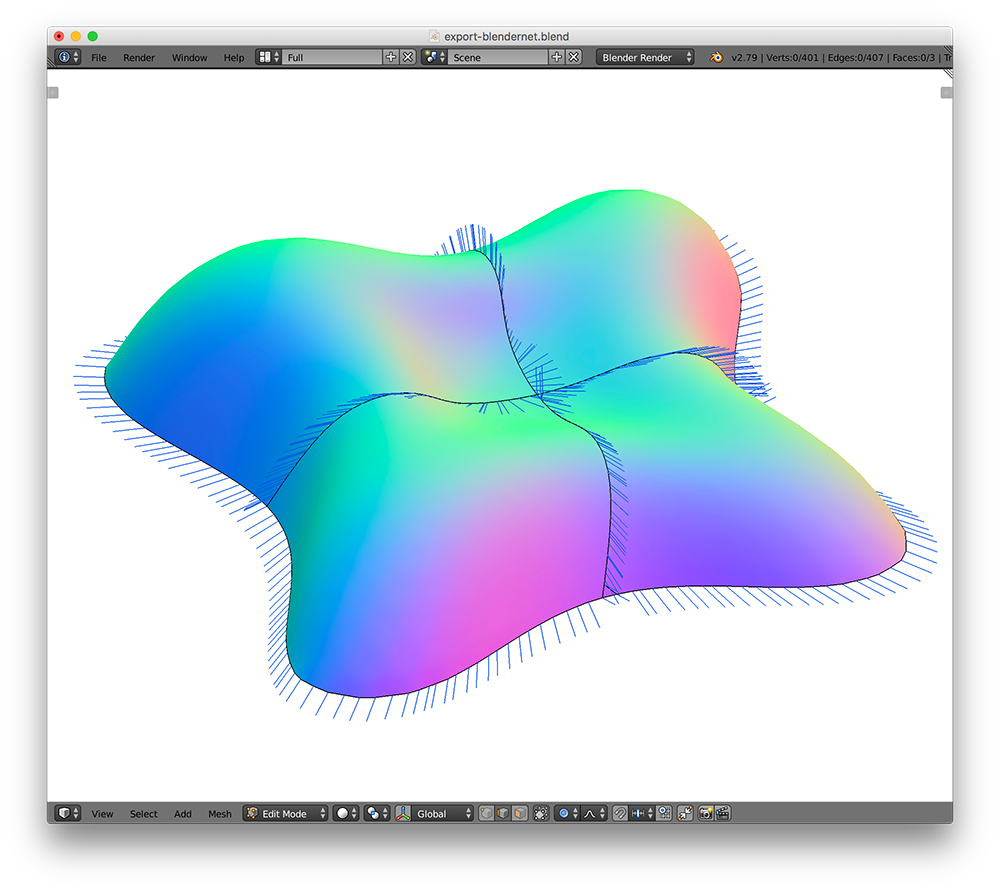
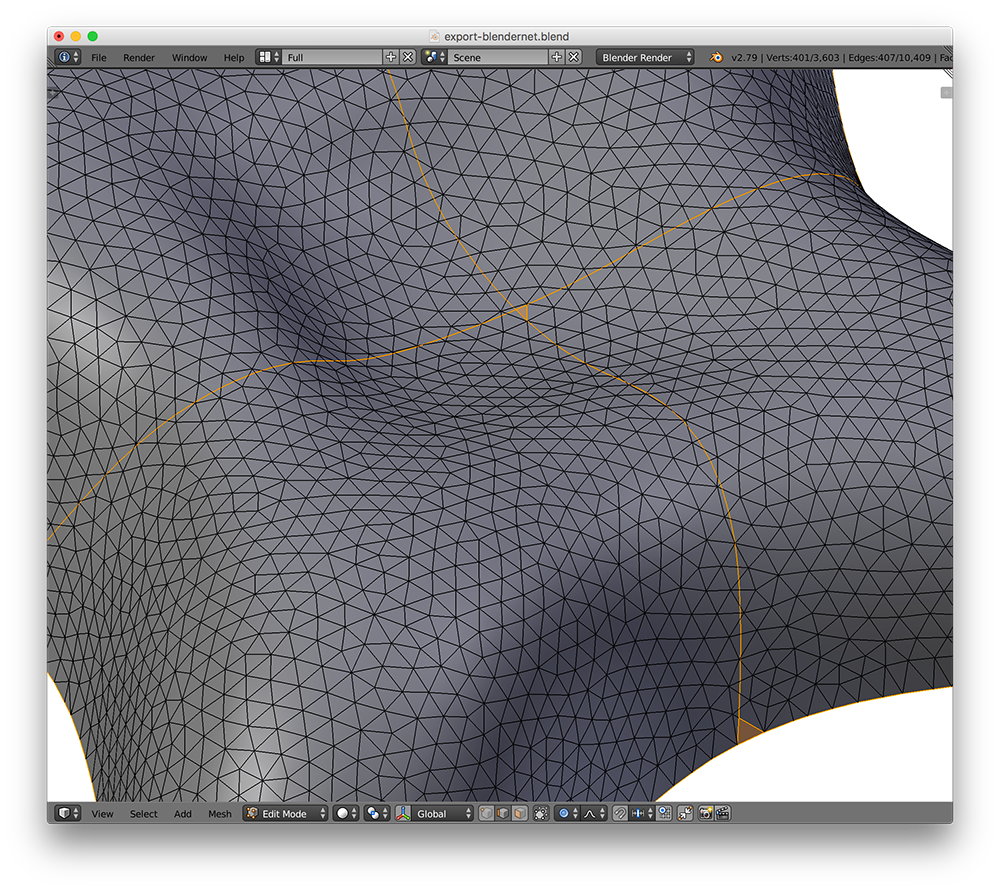
How to export a curve network with normals in Blender

9 April 2018 in blender

Most curve network datasets found online contain only positions and not surface normals along the curves (Cycles, True2Form, ILoveSketch). When I needed to create a bunch of synthetic curve networks with normals to test our surfacing algorithm, I thought this could be easily done using Blender:

Select the network on a mesh
Separate the network from the mesh using the Separation tool (P)
Export the network as an OBJ file (including the normals)

It turned out to be much more tricky than that.

The problem is to export the right normals. The above approach doesn’t work since Blender recomputes the normals after applying the Separation tool, and the new normals along the curve network are not the surface normals.

By separating the curve network from the surface, Blender messes up the normals.
Also, exporting all curves at once produces unwanted edges around intersections.

A brute-force solution might be to export the network and the mesh into separate files, then assign the normals to network vertices by matching them to mesh vertices using positions. This is not very efficient. Also – quite importantly – it does not resolve more subtle problems resulting from the triangle mesh representation, such as exporting unwanted edges around curve intersections.

Instead, I’ve written a short python script to export the curves directly. Each curve in the network is stored as a unique vertex group. Here’s the gist of it, I’ve put the complete script on github.

def getBlenderNetwork(name,groups):
  # getBlenderNetwork(dname,groups) – export a curve network with normals
  #
  # Input :
  #   [String]       name    name of the mesh with traced network on it   
  #   [Strings]      groups  list of vertex groups representing a curve network
  #
  # Output :
  #   [#Vx3, float]  V       positions of vertices in the network
  #   [#Vx3, float]  N       normals of vertices in the network
  #   [#Ex4, int]    E       edge matrix with columns
  #                            0 : curve index
  #                            1 : True=boundary edge, False=interior edge
  #                            2 : index of first vertex
  #                            3 : index of second vertex
  #
  # Author : Tibor Stanko [https://tiborstanko.sk/]
  #

    # get mesh by the name
    obj = bpy.data.objects[name]
    mesh = obj.data

    # number of curves = number of vertex groups
    nc = len(groups)

    # switch to edit mode
    bpy.ops.object.mode_set(mode='EDIT')

    # get bmesh representation
    bm = bmesh.from_edit_mesh(mesh)

    # init set of vertices
    verts = set()
    # init set of sets of edges (one set for each curve)
    edges = [set() for c in range(nc)]

    # iterate through vertex groups
    c=0
    for group in groups:
        # deselect all vertices
        bpy.ops.mesh.select_all(action='DESELECT')
        # set current vertex group to active
        bpy.ops.object.vertex_group_set_active(group=str(group))
        # select vertices in the the active group
        bpy.ops.object.vertex_group_select()
        # get all currently selected verts
        verts.update( v.index for v in bm.verts if (v.select and not v.hide) )
        # get all currently selected edges
        edges[c].update( e.index for e in bm.edges if (e.select and not e.hide) )
        # deselect the current vertex group
        bpy.ops.object.vertex_group_deselect()
        # move on to the next curve
        c+=1

    # show the updates in the viewport
    bmesh.update_edit_mesh(mesh, True)

    # number of vertices
    nv = len(verts)

    # number of edges in each curve
    ne = np.zeros(nc)
    for c in range(nc) :
        ne[c] = len(edges[c])

    # total number of edges
    ne_total = int(np.sum(ne))

    # init matrices : positions, normals, edges
    V = np.zeros((nv,3))
    N = np.zeros((nv,3))
    E = np.zeros((ne_total,4),dtype=int)

    # vertices : loop, store global (mesh) indices
    mesh_index = []
    r=0
    while len(verts) > 0 :
        # get next vertex
        v = verts.pop()
        # save global index
        mesh_index.append(v)
        # store position
        V[r,0] = bm.verts[v].co[0]
        V[r,1] = bm.verts[v].co[1]
        V[r,2] = bm.verts[v].co[2]
        # store normal
        N[r,0] = bm.verts[v].normal[0]
        N[r,1] = bm.verts[v].normal[1]
        N[r,2] = bm.verts[v].normal[2]
        # move on
        r+=1

    # edges : loop over curves (= vertex groups)
    r=0
    for c in range(nc) :
        # loop over edges in curve c
        while len(edges[c]) > 0 :
            # get next edge
            e = edges[c].pop()
            # is boundary?
            bd = len( bm.edges[e].link_faces ) == 1
            # vertices : indices in the mesh
            v0 = bm.edges[e].verts[0].index
            v1 = bm.edges[e].verts[1].index
            # vertices : indices in the curve network
            g0 = mesh_index.index(v0)
            g1 = mesh_index.index(v1)
            # store edge data : curve index, is boundary?, vertex indices
            E[r,0] = c
            E[r,1] = bd
            E[r,2] = g0
            E[r,3] = g1
            # move on
            r+=1

    return V,N,E