Surfacing curve networks with normal control

Tibor Stanko^1,2, Stefanie Hahmann², Georges-Pierre Bonneau², Nathalie Saguin-Sprynski¹

¹ CEA, LETI, MINATEC Campus, Université Grenoble Alpes

² Université Grenoble Alpes, CNRS (Laboratoire Jean Kuntzmann), Inria

2016, Computers & Graphics

teaser Surfacing curve networks with normal control

Recent surface acquisition technologies based on microsensors produce three-space tangential curve data which can be transformed into a network of space curves with surface normals. This paper addresses the problem of surfacing an arbitrary closed 3D curve network with given surface normals. Thanks to the normal vector input, the patch finding problem can be solved unambiguously and an initial piecewise smooth triangle mesh is computed. The input normals are propagated throughout the mesh. Together with the initial mesh, the propagated normals are used to compute mean curvature vectors. We then compute the final mesh as the solution of a new variational optimization method based on the mean curvature vectors. The intuition behind this original approach is to guide the standard Laplacian-based variational methods by the curvature information extracted from the input normals. The normal input increases shape fidelity and allows to achieve globally smooth and visually pleasing shapes.

Downloads

paper ~ 16.7 MB

Video

Acknowledgments

This research was partially funded by the ERC advanced grant no. 291184 EXPRESSIVE.

BibTeX

@article{ Stanko:2016:CAG,
  title = {Surfacing curve networks with normal control},
  author = {Tibor Stanko and Stefanie Hahmann and Georges-Pierre Bonneau and Nathalie Saguin-Sprynski},
  journal = {Computers \& Graphics},
  publisher = {Elsevier},
  volume = {60},
  pages = {001-008},
  month = {11},
  year = {2016},
  doi = {10.1016/j.cag.2016.07.001}
}

Supplementary material

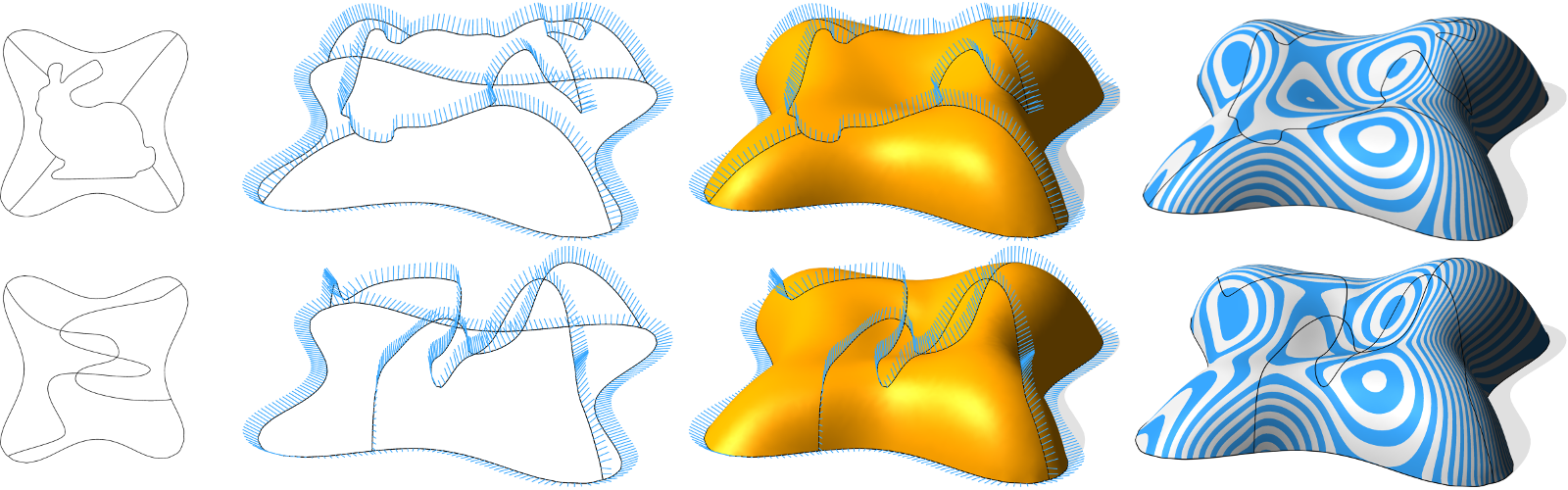
The following is a comparison of [Pan et al., 2015] (left surfaces) with our method (right surfaces). These figures are not a part of our paper.

To better see the differences between the computed surfaces, we use normal mapping on a circle-symmetric texture as shown below. This texture is useful for examining continuity, regularity and symmetry of the reconstructed shapes.

The algorithm of [Pan et al.] does not preserve the symmetry of the input network in the computed surface. Our algorithm keeps the symmetry: the final textured surfaces are fairly regular and the circles are preserved in the texture.