Refining procedures on mesh via algebraic fitting
A new nonlinear refinement algorithm for surfaces is presented in this work. Our scheme operates on triangular meshes and interpolates input data. Each triangle is associated with a small set of neighbouring points and normals. A low degree algebraic surface (quadric) is fitted to this set with respect to the chosen objective function. The new vertex is taken from the computed quadric. Such a setup overcomes the limitations of the linear schemes. Our experiments show the scheme might be capable of reconstructing quadratic surfaces from a coarse approximating mesh. A comparison of the proposed method with the linear schemes is shown, as well as an application to the compression of a large-scale mesh.
Downloads
- paper ~ 2.4 MB
BibTeX
@inproceedings{ Stanko:2014:CESCG,
title = {Refining procedures on mesh via algebraic fitting},
author = {Tibor Stanko and Pavel Chalmovianský},
booktitle = {Proc. CESCG 2014},
editor = {M. Wimmer and J. Hladůvka and M. Ilčík},
isbn = {978-3-9502533-6-8},
month = {April},
year = {2014}
}
Choosing the weights
The proposed method allows the specification of the weights for each vertex. We demonstrate the effect of different sets of weights on the Stanford bunny.


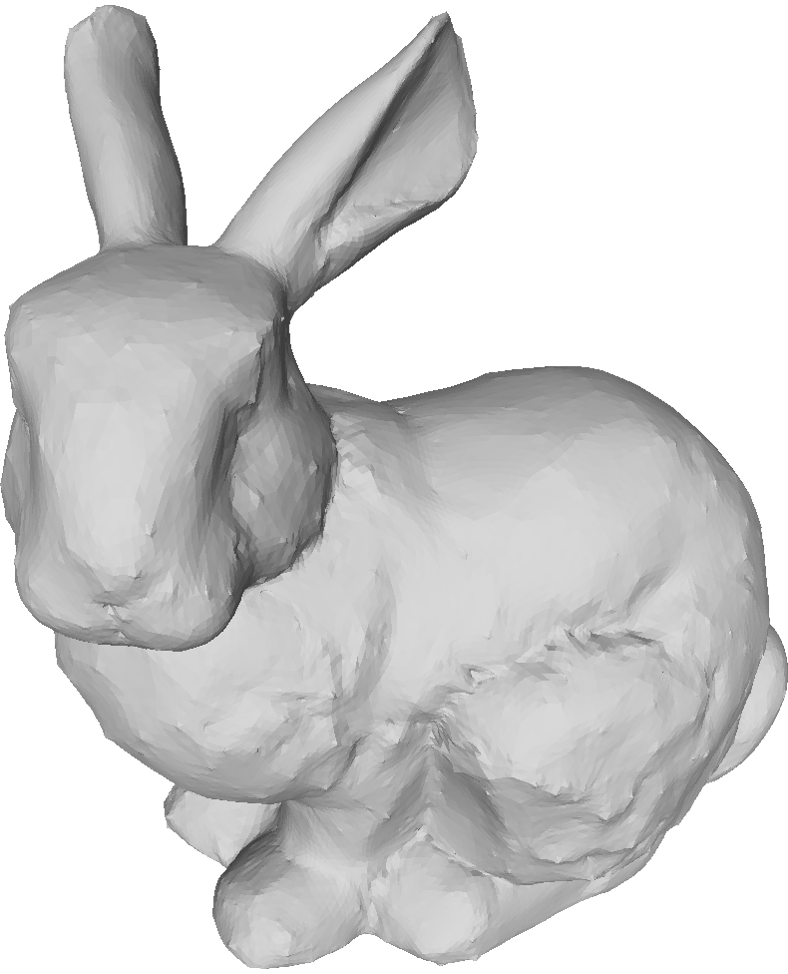

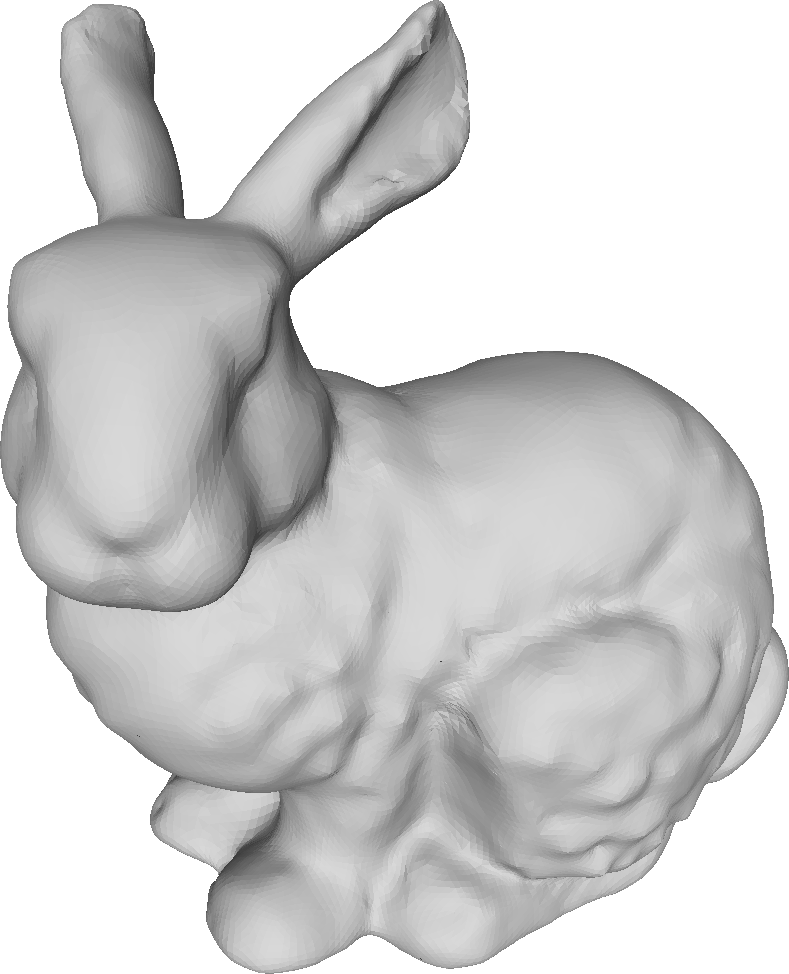
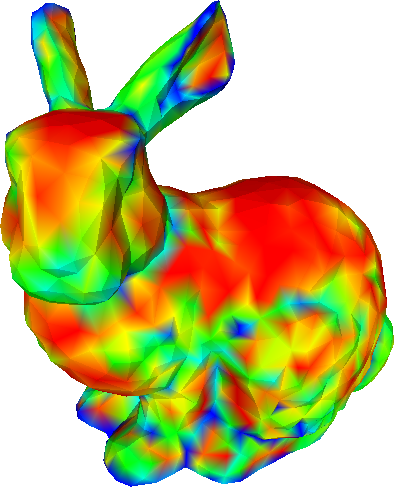
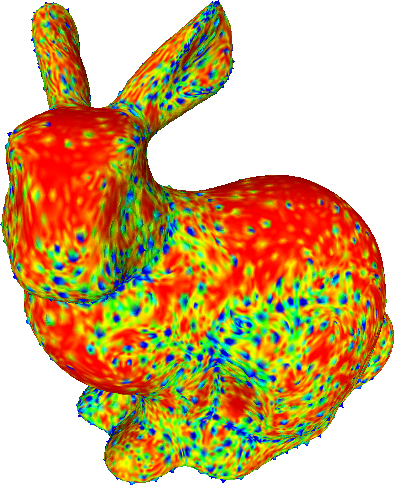
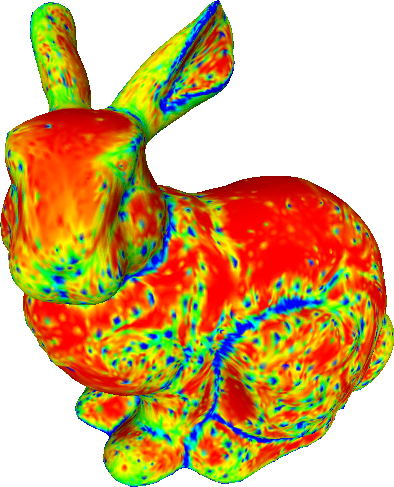
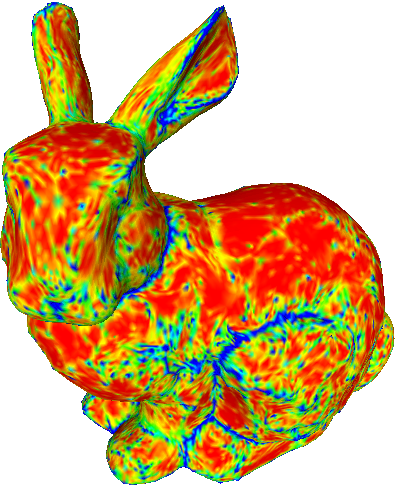

Bunny refined with various sets of weights.
Bottom row shows the curvature (red = smaller, blue = higher).
The influence of normals
To show how the change in the prescribed normals influences the limit surface, we applied our method on the Stanford bunny with alternative set of vertex normals. This alternative set of normals was generated randomly from a noise function.

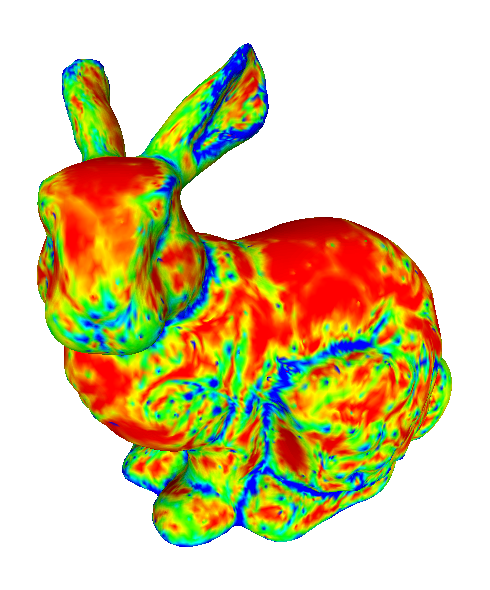
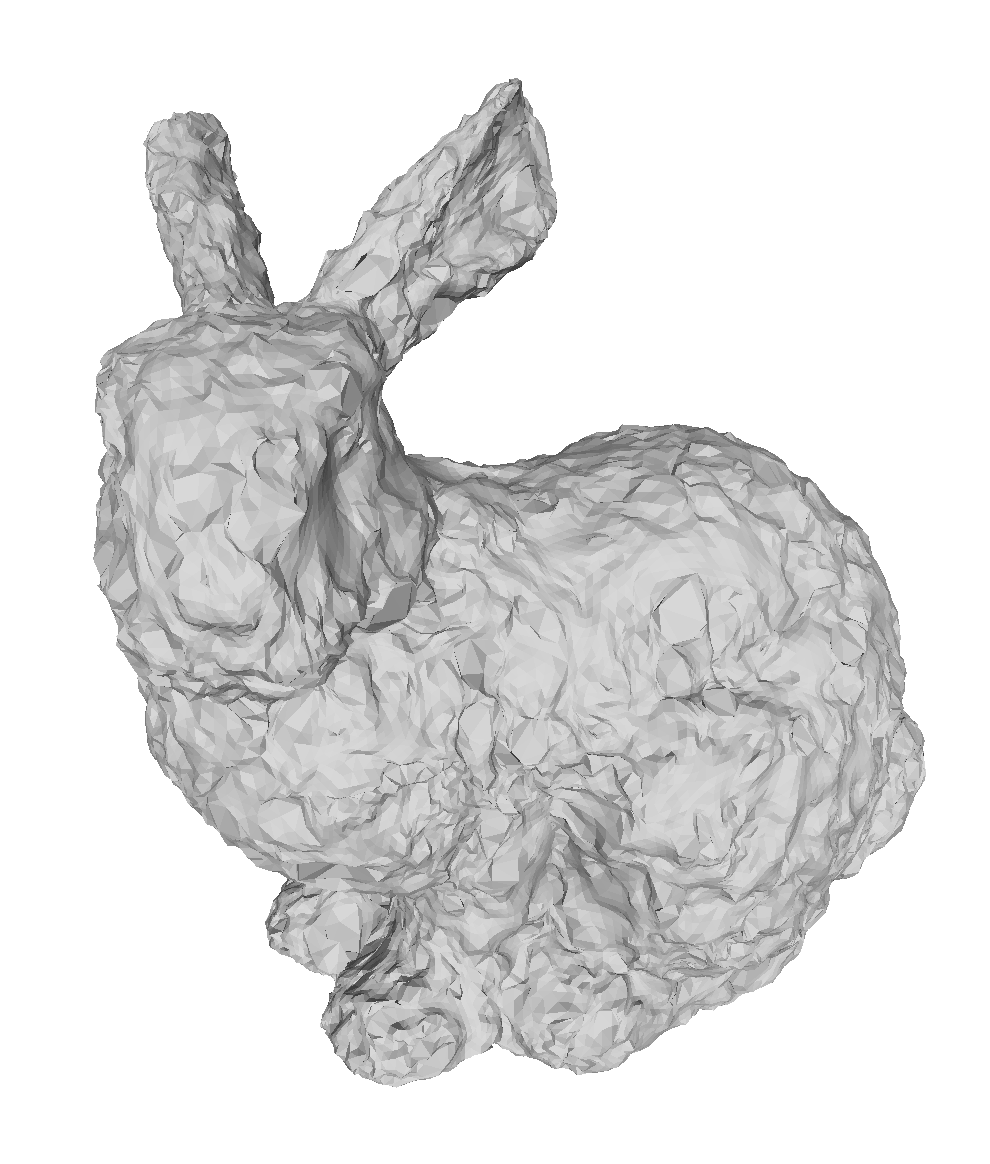
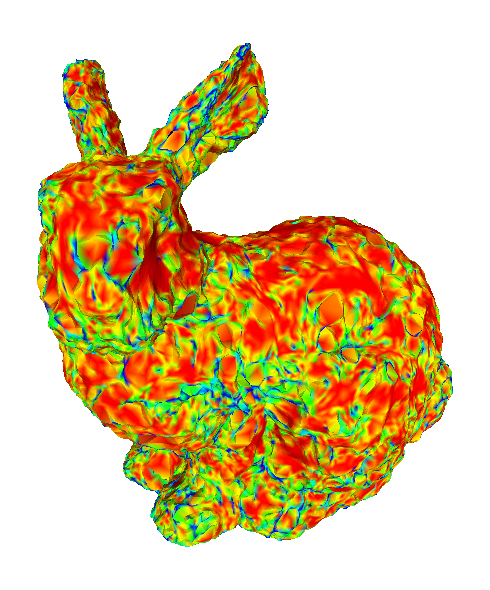
Left: original normals. Right: random normals.
Comparison with linear schemes
To compare the proposed algorithm with the linear schemes, we have used the large-scale mesh of the Venus of Dolní Věstonice. This mesh is a discretized version of the small nude female statuette found in Moravia south of Brno. Dated to 29,000-25,000 BCE, it is considered one of the oldest known pieces of ceramic in the world.

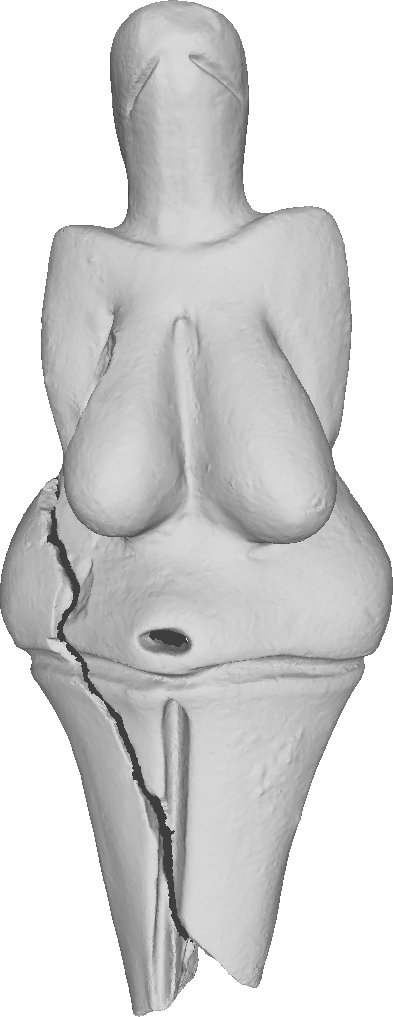

Left: the statuette dating to 29,000-25,000 BCE.
Middle: scanned mesh, 131114 vertices.
Right: decimted mesh, 1356 vertices.
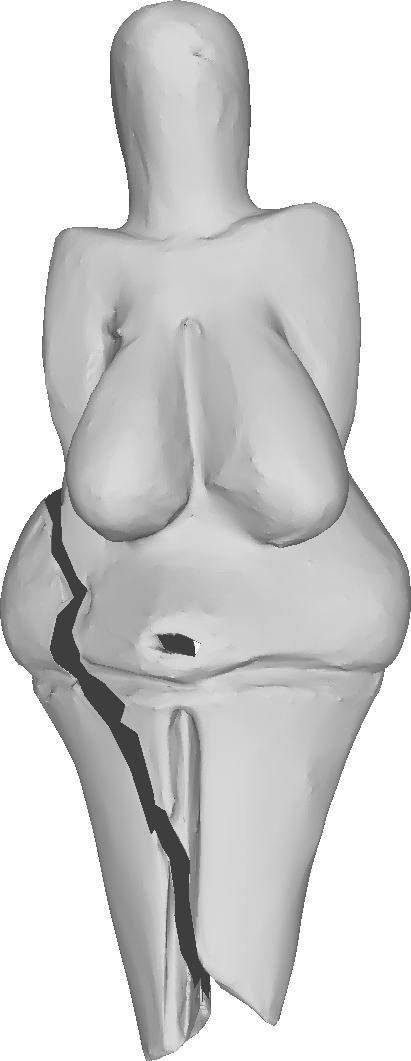
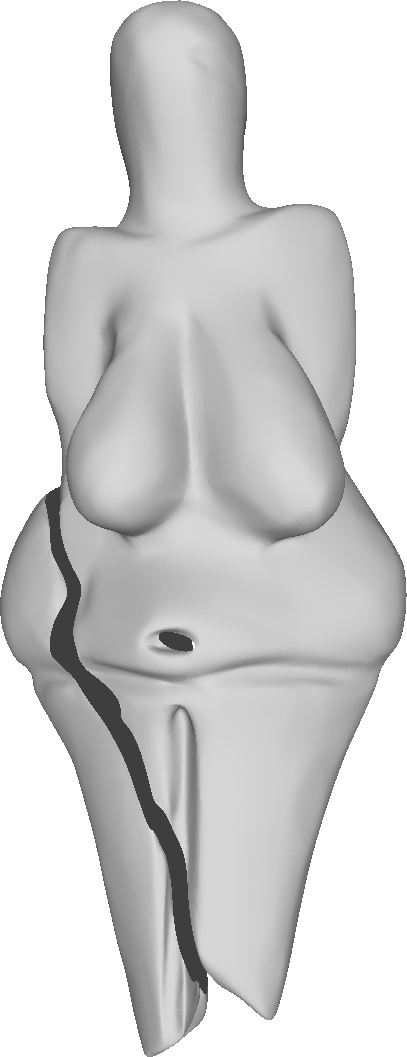
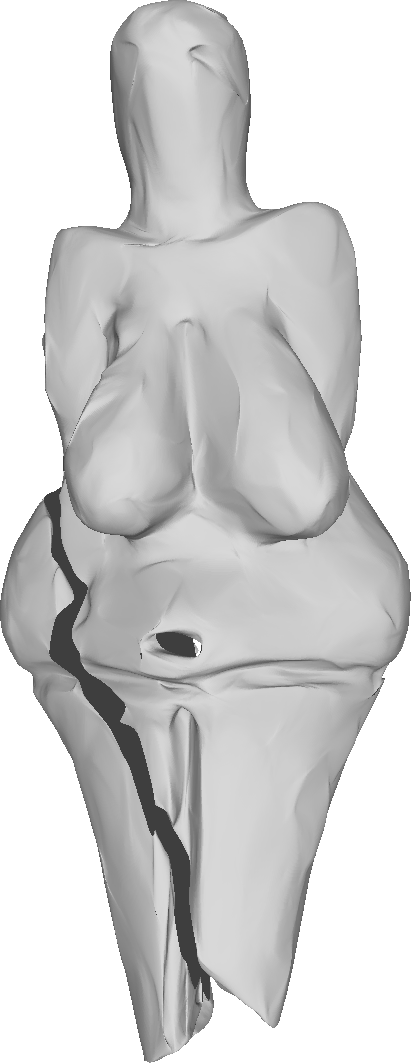
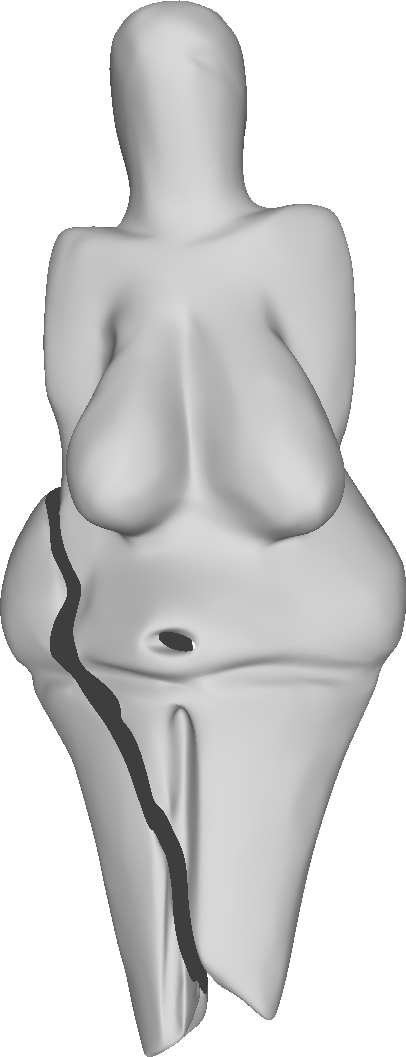
The decimated mesh refined four times.
Left to right: our method, √3-subdivision, Modified butterfly, Loop.
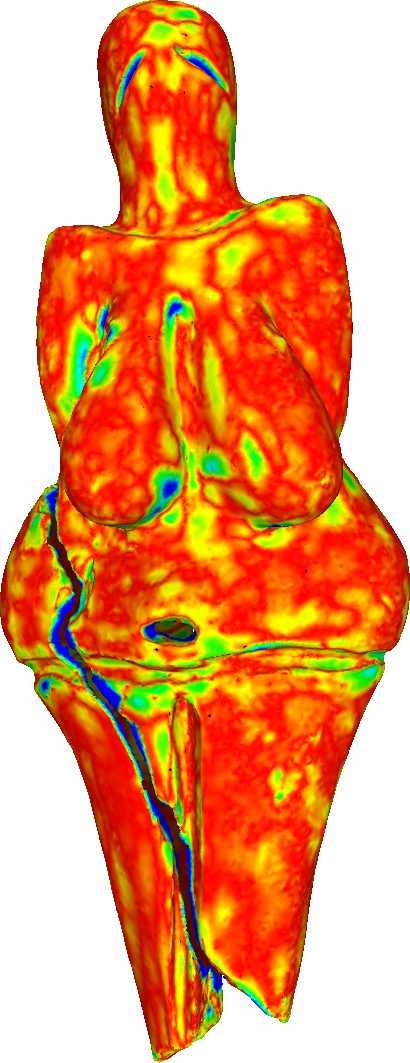
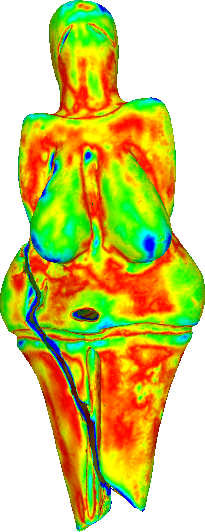
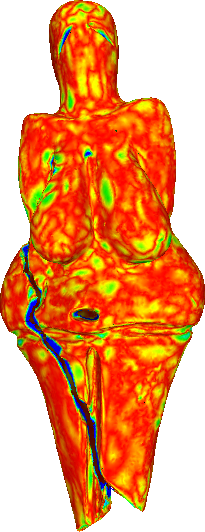
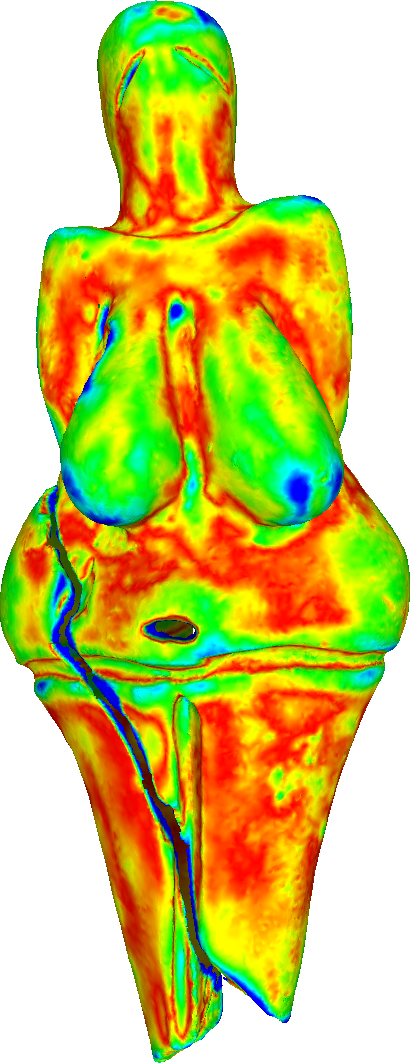
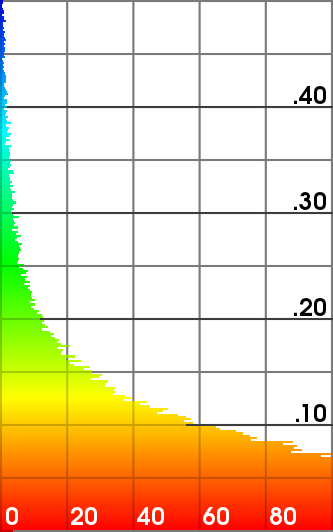
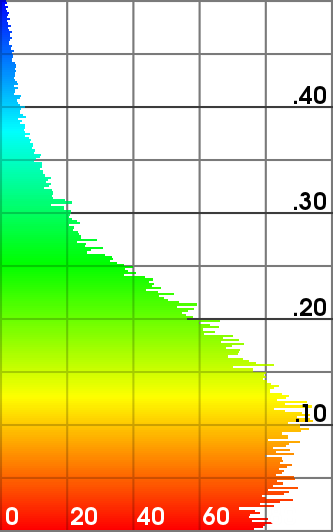
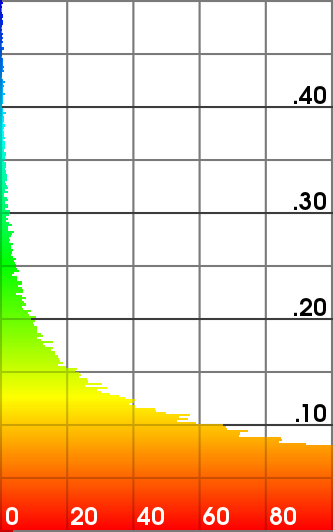
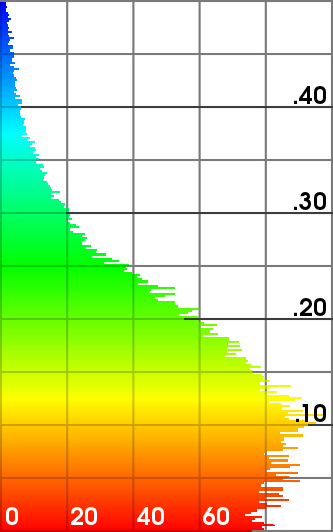
Hausdorff distance of the refined meshes from the ground truth (scanned mesh).
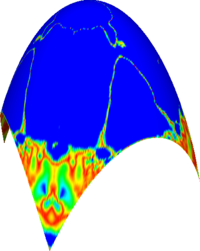
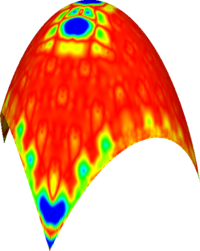
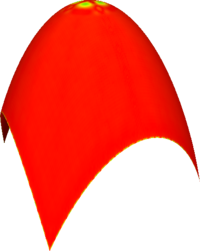
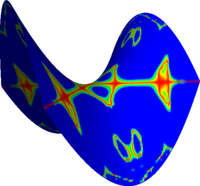
Reconstruction of quadratic surfaces
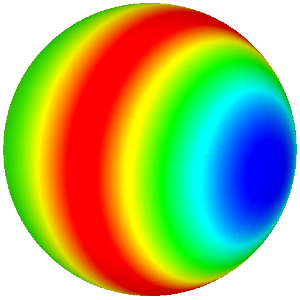
The proposed method can also be used to reconstruct quadratic surfaces from a coarse approximating mesh. For instance, with the right choice of weights, it is possible to reconstruct a close approximation of the units sphere from the cube. The initial mesh along with the first 8 iterations is shown below. The last picture is the visualisation of the Hausdorff distance of the limit surface from the original sphere. [red = zero distance, blue = distance ≥ 0.0025 units]
Sphere









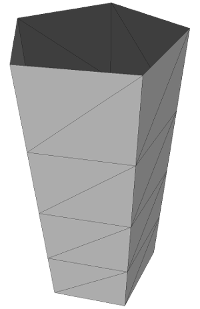
Cylinder

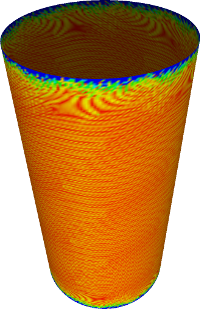


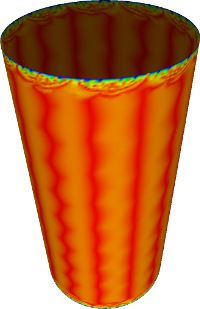



Elliptic paraboloid
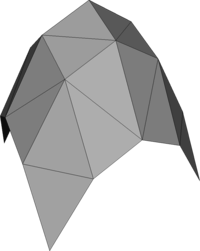
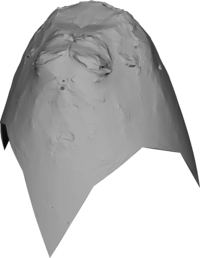




Hyperbolic paraboloid






Implementation
The proposed method was implemented using OpenMesh and Armadillo. All figures were created in MeshLab.