git remote | xargs -L1 git push --all

[source]

Here’s a simple example for gif screencasting with byzanz. See the thread How to create animated GIF images of a screencast? on askubuntu.com.

byzanz-record --duration=12 --x=725 --y=365 --width=487 --height=375 out.gif

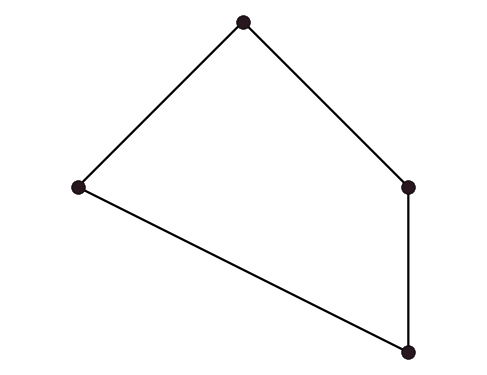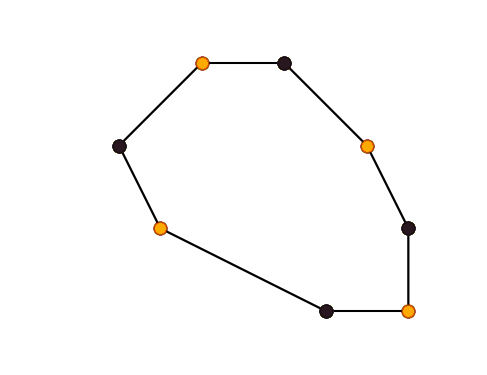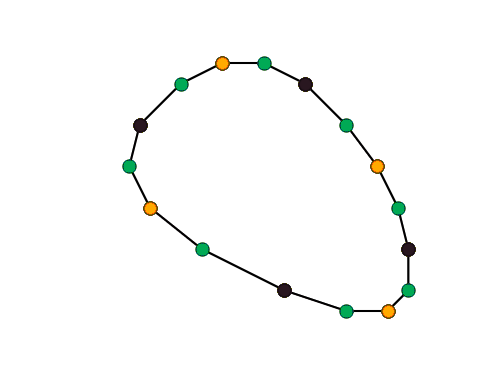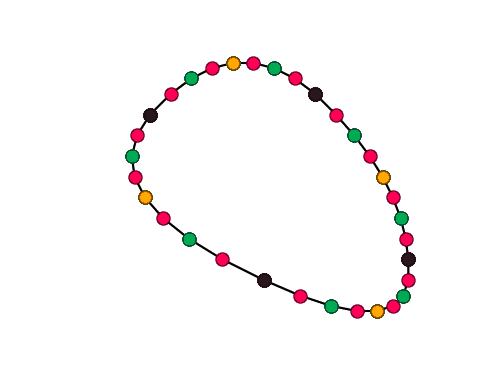
Animation of Chaikin curve subdivision scheme captured with byzanz.

On Fedora, byzanz can be installed from the official repo.

sudo dnf install byzanz

We got this giant plastic lilium for the tests of our sensor surface reconstruction. Looking forward to the experiments!

(The small device in the middle is the Morphorider.)

Multiplicities of array elements can be efficiently computed using sparse. I’ve found this elegant solution in an old Newsgroup thread.

% generate some data
A = randi(10,1,100);
% construct the sparse matrix
S = sparse(A,1,1);
% get unique elements and multiplicities
[uA,~,mult] = find(S);

mult =
   (1,1)        8
   (2,1)       15
   (3,1)       11
   (4,1)        5
   (5,1)       10
   (6,1)        6
   (7,1)       10
   (8,1)       13
   (9,1)       13
  (10,1)        9

This method is faster than other solutions – almost twice as fast as histc.

% test array: 2000 random integers from the set 1:1000
% 1000 iterations
Elapsed time is 0.228704 seconds. % histc
Elapsed time is 1.838388 seconds. % bsxfun
Elapsed time is 0.128791 seconds. % sparse

Once upon a time, I heard a song. This one:

Naturally, I had to tab it. And it remained the only tab I’ve ever published.

Then I kind of forgot about it.

Recently, I was searching for some stuff on UG (Ultimate Guitar, not University of Grenoble…) and wondered what happened to my tab. To my surprise, not only did it have some views, it was also rated as excellent! That felt good.

Strange thing, this tabbing. Are you actually creating something new when tabbing somebody else’s song? To put it another way, are you inventing or discovering?

Anyway, I’ll try to post more of tabs from now on. Of this song, for instance.

And I definitely need to practice more.

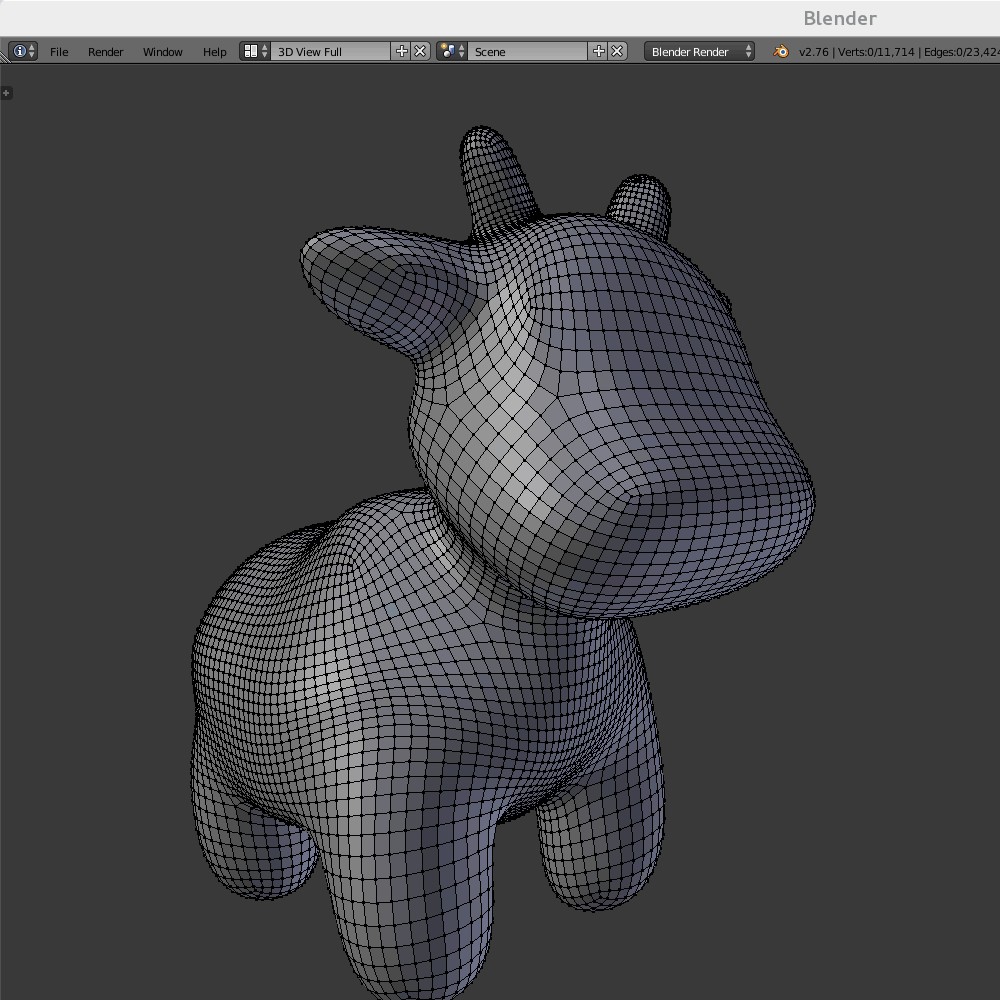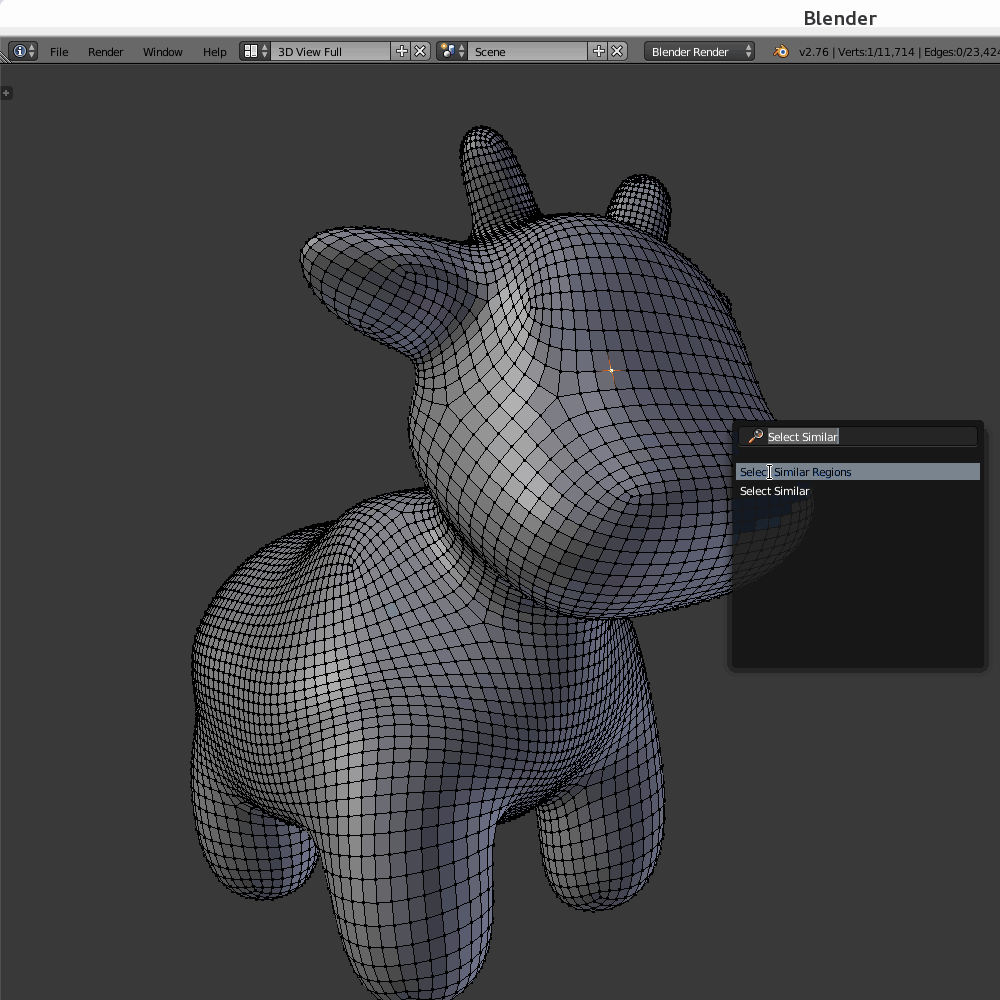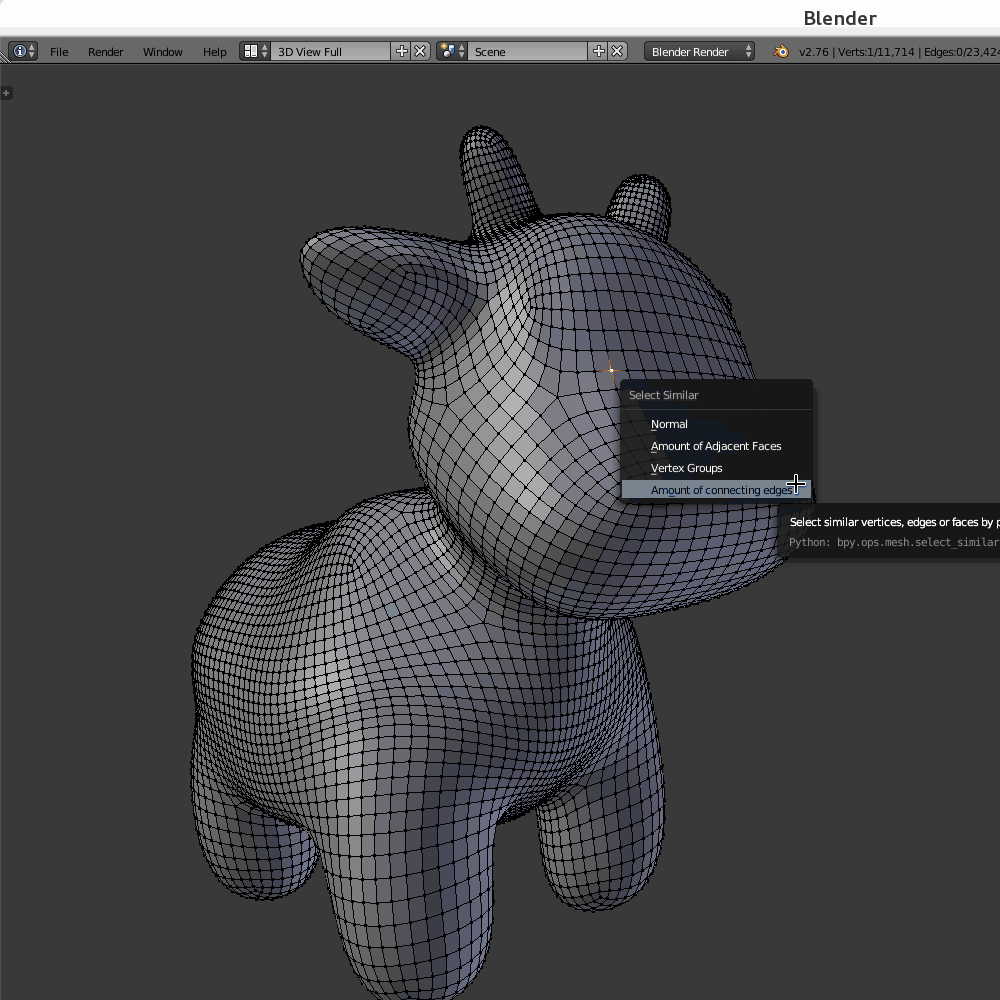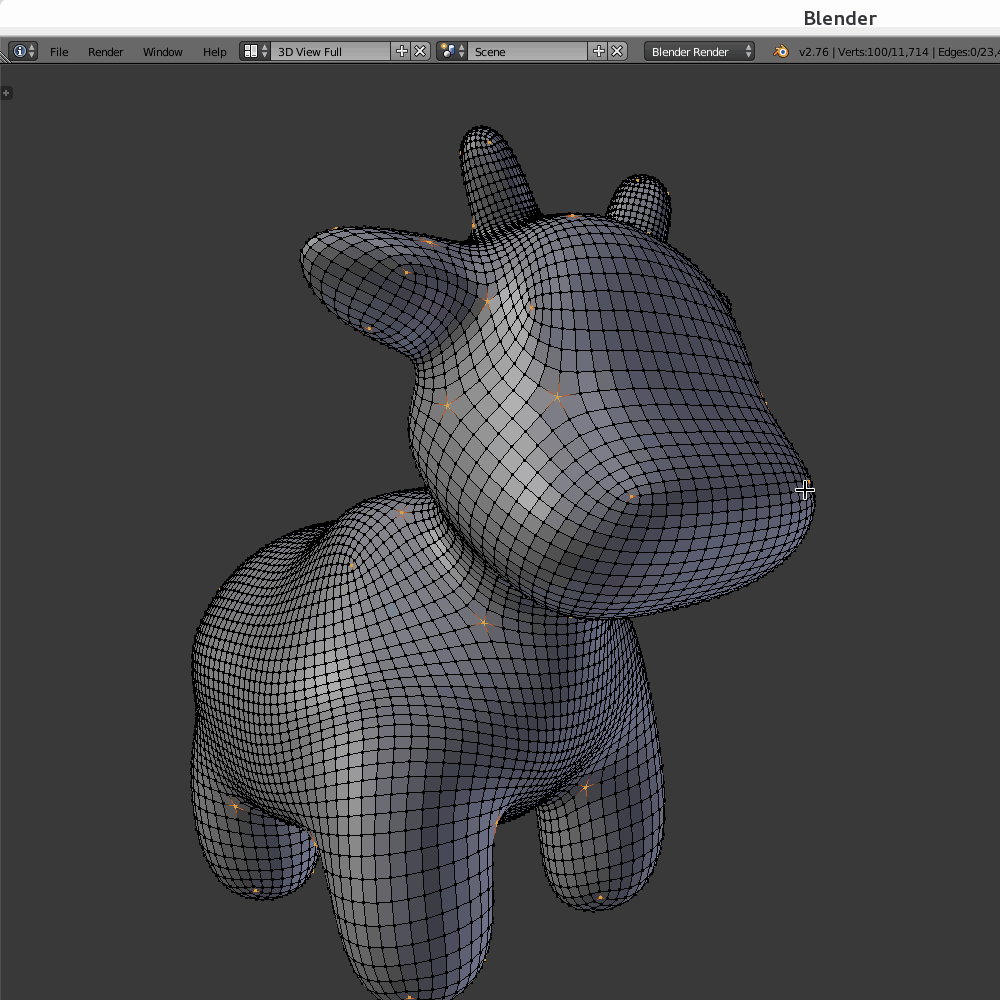
Extraordinary vertices in a polygon mesh are the ones which are not regular – their degree is other than 6 in a triangle mesh and other than 4 in a quad mesh. Here’s how to select all extraordinary mesh vertices in Blender:

1. Select a regular vertex.
2. Select->Select Similar->Amount of connecting edges.
   This will select all regular vertices.
3. Hit Ctrl+I to invert the selection.