Tibor Stanko
TP9 submission deadline is Thursday, 13/04/2017 at 23:59. The TP on Friday 14/04 will start at 13:30 (instead of 15:15).

.geonum2017

  1. Bézier curves
  2. Bézier splines
  3. B-splines
  4. Subdivision curves
  5. Lane-Riesenfeld
  6. Bézier surfaces
  7. B-spline surfaces
  8. Subdivision B-surfaces
  9. Triangle mesh subdivision

TP3 : B-splines, De Boor's algorithm

17 February 2017 in

Code

B-splines cheatsheet

  • degree k
  • n + 1 control points
  • m + 1 knots
  • m = n + k + 1

B-splines

Downside of Bézier splines is their global nature: moving a single control point changes the whole spline. A possible solution to this issue are the B-splines.

Given a degree $k$, control polygon $\mathbf d_0,\dots,\mathbf d_n$, and a knot vector $t_0 \leq t_1 \leq \dots \leq t_m$ with $m = n+k+1$, a B-spline curve $S(t)$ is defined as

\[S(t) = \sum_{j=0}^n \mathbf d_j N_j^k(t), \quad t\in[t_k, t_{n+1}).\]

The $N_j^k$ are the recursively-defined basis functions (hence the name B-spline)

\[\begin{array}{ll} N_j^{0}(t) =& \begin{cases} 1 \quad t\in[t_j, t_{j+1}) \\ \\ 0 \quad \text{ otherwise } \end{cases} \\ \\ N_j^k(t) =& \underbrace{ \frac{ t - t_j }{ t_{j+k} - t_j } }_{ w_{j,k}(t)} N_j^{k-1}(t) + \underbrace{ \frac{ t_{j+k+1} - t}{ t_{j+k+1} - t_{j+1} } }_{1 - w_{j+1,k}(t)} N_{j+1}^{k-1}(t) \end{array}\]

Looks complicated? Don’t worry if you cannot get your head around all the indices and whatnot; De Boor is here to help you!

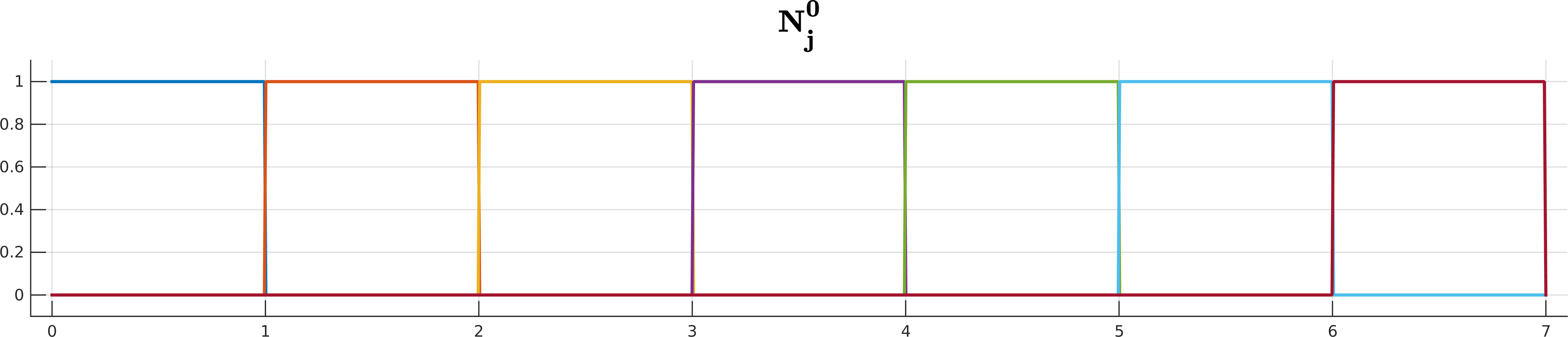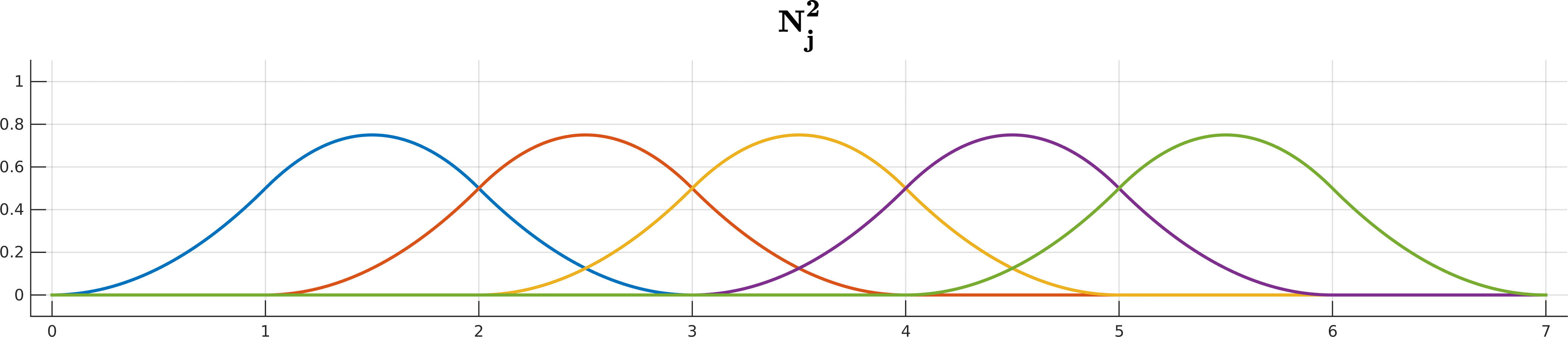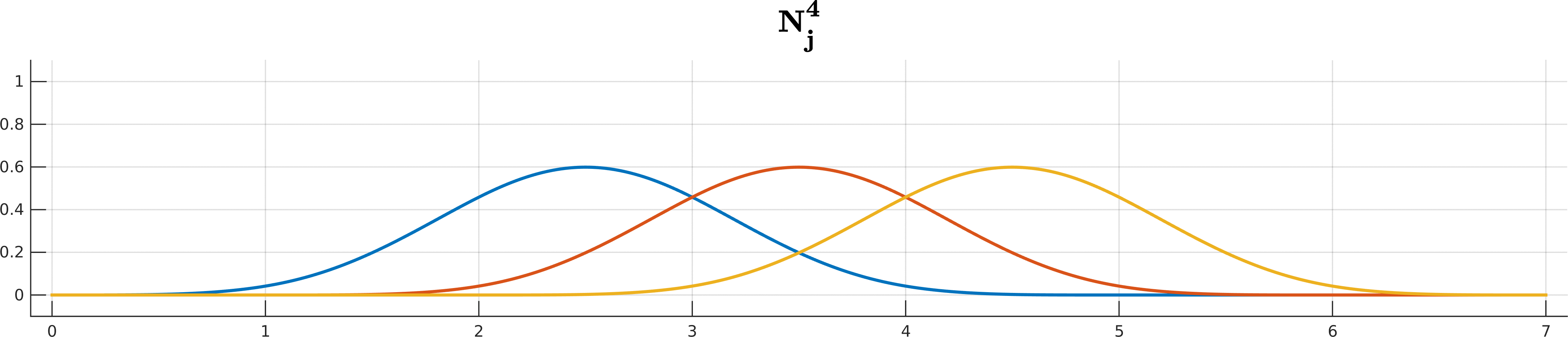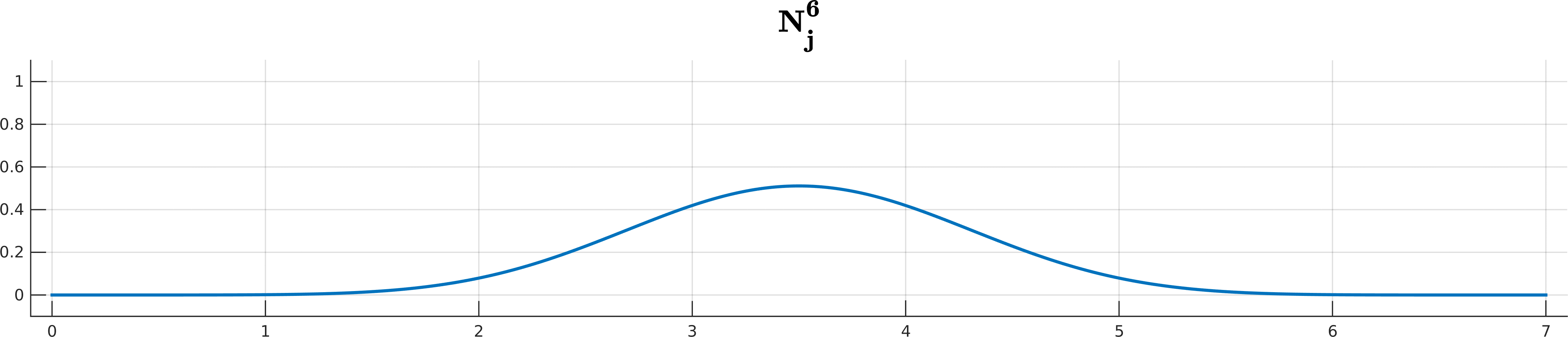
B-spline Basis

B-spline basis functions $N^k_j$ up to degree 5 for the knot sequence $(0,1,2,3,4,5,6,7)$.

De Boor’s algorithm

… also called the De Boor-Cox algorithm can be seen as a generalization of the De Casteljau’s algorithm. (Bézier curve is in fact a B-spline with a special knot sequence.)

  • input : $\mathbf{d_{0}},\dots,\mathbf{d_{n}}$ : control points
    $t_0 \leq t_1 \leq \dots \leq t_m$ : knot vector
    $t \in [t_i, t_{i+1}) \subset [t_k, t_{m-k})$ where $k = m-n-1$ is the degree
  • output :   point $\mathbf S(t) = \mathbf d_i^k$ on the curve
  • algorithm : For $j=i-k, \dots, i,$ set $\mathbf d_j^0 = \mathbf d_j$. Then compute the points \begin{align} \mathbf d_{j}^{r} &= (1-w_{j,k-(r-1)}) \mathbf d_{j-1}^{r-1} + w_{j,k-(r-1)} \mathbf d_{j }^{r-1} \end{align} for \begin{align} \quad r = 1,\dots,k, \quad \quad j = i-k+r,\dots,i \end{align} with \begin{align} w_{j,k-(r-1)} &= \frac{ t - t_j }{ t_{j+k-(r-1)} - t_j }. \end{align}

Be careful with the indices! Here we have expressed a point at depth $r$ in terms of points at depth $r-1$ – that is why there is the $r-1$ everywhere in the formula.

This might be a bit annoying, but I think it’s also more practical for the recursive implementation. (The formula becomes much more elegant if we express level $r+1$ in terms of level $r$.)

spiral1 spiral2

A cubic B-spline with 16 segments and endpoint interpolation.

ToDo$^1$

  1. Implement the De Boor’s algorithm.
  2. Evaluate B-spline for the simple dataset. Modify the knot vector and recompute. What changed?
  3. Evaluate B-spline for the spiral dataset. Modify the knot vector to 0 0 0 0 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 5 5 5. What changed?
  4. Evaluate B-spline for the camel dataset. Move the front leg by changing the x-coordinate of the last control point to -1.5. Which segments of the curve have changed? Why?

NURBS

If you’ve tested with the circle.bspline dataset, you were probably dissapointed: the resulting curve is far from being a circle.

Here’s the bad news: it’s mathematically impossible to represent circle as a B-spline. But, it is possible via a generalization called Non-Uniform Rational B-Splines or NURBS.

Why the long name? Non-uniform simply means the knot sequence is non-uniformly spaced. Rational means we work in homogeneous coordinates by assigning a weight to each point.

In plane, the point $(x,y)$ becomes $(x,y,1) \approx (wx,wy,w)$.

If you examine circle9.nurbs file, you’ll it’s quite similar to circle.bspline. The only thing that’s changed is the addition of a third coordinate – this is the weight w.

And here’s the good news: even with the homogeneous coordinates, we can apply exactly the same De Boor’s algorithm without any modifications!

Here’s a secret recipe for transforming your B-spline code to work with NURBS:

  1. The columns of ControlPts read from a .nurbs correspond to x, y and w. Therefore, you first need to multiply both x and y (columns 0 and 1) by w (column 2).
  2. Feed the homogeneous control points [w*x,w*y,w] to the De Boor’s algorithm you’ve implemented previously.
  3. Convert the computed points (stored in the matrix Segment) back to Cartesian coordinates. Divide by the third column to pass from [w*x,w*y,w] to [x,y,1].
  4. As before, plot the first two coordinates.

Hint: in Python, the operators * and / are applied element-wise, so you can do stuff like

matrix[:,0] *= matrix[:,2]
matrix[:,0] /= matrix[:,2]

ToDo$^2$

  1. Modify your code to work in homogeneous coordinates (if dim=3).
  2. Evaluate circle9.nurbs and circle7.nurbs. Compare the results with circle.bspline.

Resources