Tibor Stanko
TP9 submission deadline is Thursday, 13/04/2017 at 23:59. The TP on Friday 14/04 will start at 13:30 (instead of 15:15).

.geonum2017

  1. Bézier curves
  2. Bézier splines
  3. B-splines
  4. Subdivision curves
  5. Lane-Riesenfeld
  6. Bézier surfaces
  7. B-spline surfaces
  8. Subdivision B-surfaces
  9. Triangle mesh subdivision

TP7 : B-spline Surfaces

24 March 2017 in

Code

B-spline curves revisited

Back in TP3, we were working with B-spline curves. A B-spline curved is defined by the following:

\[d : \text{ degree } \\ \mathbf d_{0},\dots, \mathbf d_{m} : \text{ control polygon } \\ t_{0},\dots,t_{m+d+1} : \text{ knot vector }\]

Tensor product B-spline surfaces

A B-spline surface is defined via

\[du, dv : \text{ degrees in } u, v \\ \text{ } \\ \left( \begin{array}{ccc} \mathbf d_0^0 & \dots & \mathbf d_m^0 \\ \vdots & \ddots & \vdots \\ \mathbf d_0^n & \dots & \mathbf d_m^n \end{array} \right) : \text{ control net } \\ \text{ } \\ u_0,\dots,u_{m+du+1} : \text{ knot vector in } u \\ v_0,\dots,v_{n+dv+1} : \text{ knot vector in } v\]

B-spline surface is defined for $(u,v) \in [u_{du},u_{m+1}[ \times [v_{dv},v_{n+1}[$ as

\[S(u,v) = \sum_{i=0}^m \sum_{j=0}^n \mathbf d_i^j N_{i}^{k}(u) N_{j}^{l}(v)\]

where $N$ are the basis functions (see TP3).

Surface Patches

Recall that a B-spline curve is made from many smaller pieces, defined over parameter intervals $[t_i,t_{i+1}]$. Analogically, a B-spline surface consists of patches, each defined over a parameter rectangle $[u_i,u_{i+1}] \times [v_j,v_j+1]$ :

\[\begin{array}{llll} [u_{du},u_{du+1}] \times [v_{dv },v_{dv+1}] & [u_{du+1},u_{du+1}] \times [v_{dv },v_{dv+1}] & \dots & [u_{m},u_{m+1}] \times [v_{dv },v_{dv+1}] \\ [u_{du},u_{du+1}] \times [v_{dv+1},v_{dv+2}] & [u_{du+1},u_{du+1}] \times [v_{dv+1},v_{dv+2}] & \dots & [u_{m},u_{m+1}] \times [v_{dv+1},v_{dv+2}] \\ \vdots & \vdots & \ddots & \vdots \\ [u_{du},u_{du+1}] \times [v_{n-1},v_{n }] & [u_{du+1},u_{du+1}] \times [v_{n-1},v_{n }] & \dots & [u_{m},u_{m+1}] \times [v_{n-1},v_{n }] \\ [u_{du},u_{du+1}] \times [v_{n },v_{n+1}] & [u_{du+1},u_{du+1}] \times [v_{n },v_{n+1}] & \dots & [u_{m},u_{m+1}] \times [v_{n },v_{n+1}] \\ \end{array}\]

Algorithm

We’ll evaluate and display each patch individually. The algorithm is summarized in the following pseudocode.

# loop over all patches
for i in (du,du+1,...,m) :
    for j in (dv,dv+1,...,n) :
        # check if the patch is not degenerate
        if not valid_patch :
            continue
        # loop over the samples of the current patch
        # defined over [u_i,u_i+1] x [v_j,v_j+1]
        for u in uniform_sampling( u_i, u_i+1, number_of_samples ) :
            for v in uniform_sampling( v_j, v_j+1, number_of_samples ) :
                compute_S(i,j,u,v) # a surface point on the current patch

ToDo

  1. Implement evaluation of B-spline surfaces. Test with the provided datasets (simple.bspline and torus.bspline).
  2. Modify the knot vectors for the simple dataset. Experiment with various configurations. How does the surface change?
  3. [Bonus] NURBS surfaces can be used to represent the unit sphere, the same way we used NURBS curves to represent the unit circle in TP3. Modify your implementation of B-spline surfaces to compute NURBS surfaces. Test with the hemisphere (hemi.nurbs) and the modified torus (torus.nurbs).
    Note: full sphere control points, weights, and knots can be found in Representing a Circle or a Sphere with NURBS by David Eberly.

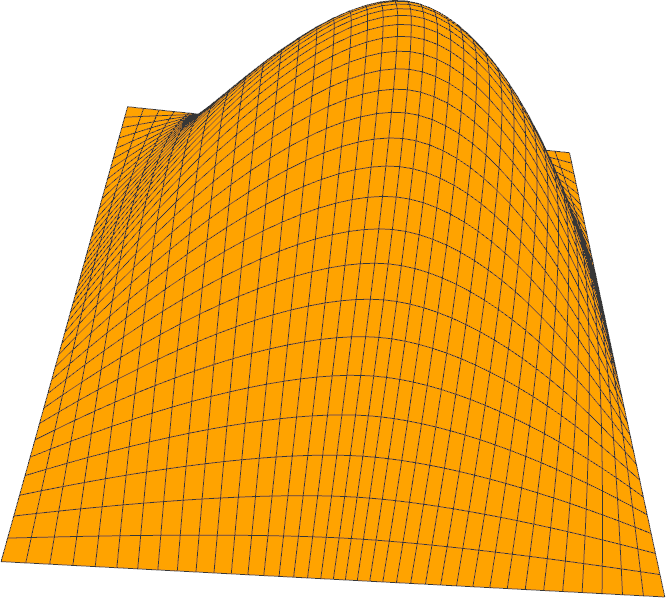
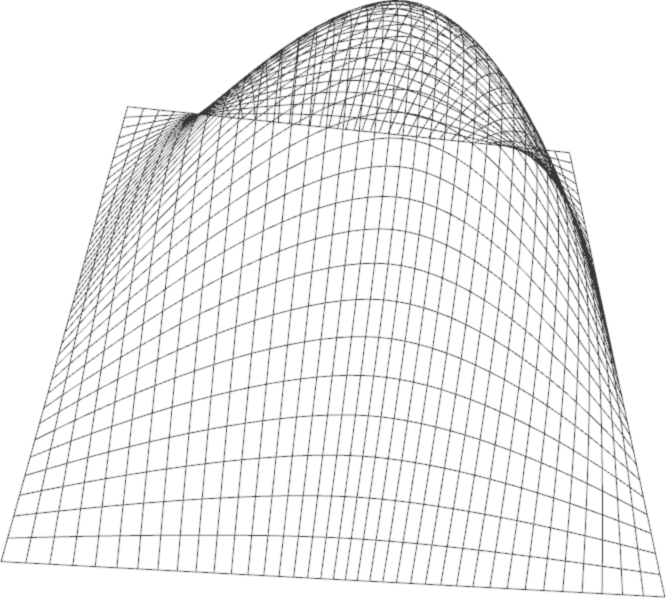
simple full simple wire

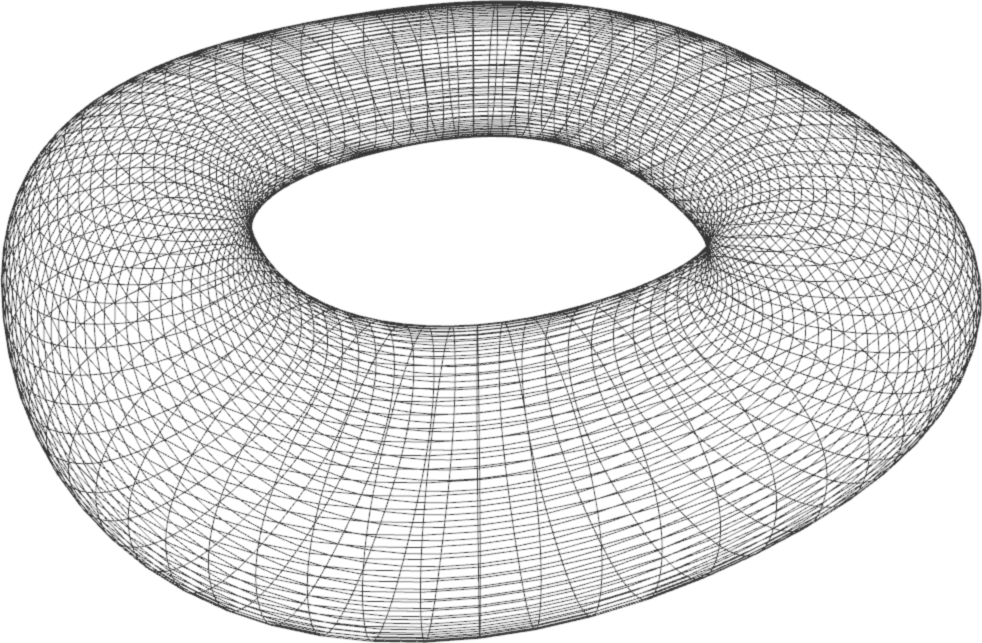
torus full torus wire

Resources