TP1 : Bézier curves, De Casteljau’s algorithm

5 February 2016 in

Bézier curves

A degree $n$ Bézier curve takes the form

\[\mathbf x(t) = \sum_{i=0}^{n} \mathbf b_i B_i^n(t) \qquad t \in [0,1]\]

where

\[B_{i}^{n}(t) = \begin{pmatrix}n \\ i\end{pmatrix} (1-t)^{n-i} t^i\]

are the degree $n$ Bernstein polynomials, and the binomial coefficients are defined as

\[\begin{pmatrix}n \\ i\end{pmatrix} = \frac{n!}{(n-i)! i!}.\]

The Bézier points $\mathbf b_i \in \mathbb R^d$ form the control polygon.

De Casteljau’s algorithm

input Bézier points $\mathbf b_i$ for $i = 0, \dots, n$, and parameter $t \in [0,1]$.
output The point $\mathbf b_0^n$ on the curve.
compute Set $\mathbf b_i^0 = \mathbf b_i$ and compute the points
\[\mathbf b_i^k (t) = (1-t) \mathbf b_i^{k-1} + t \mathbf b_{i+1}^{k-1} \qquad \text{for} \qquad k=1,\dots,n, \quad i=0,\dots,n-k.\]

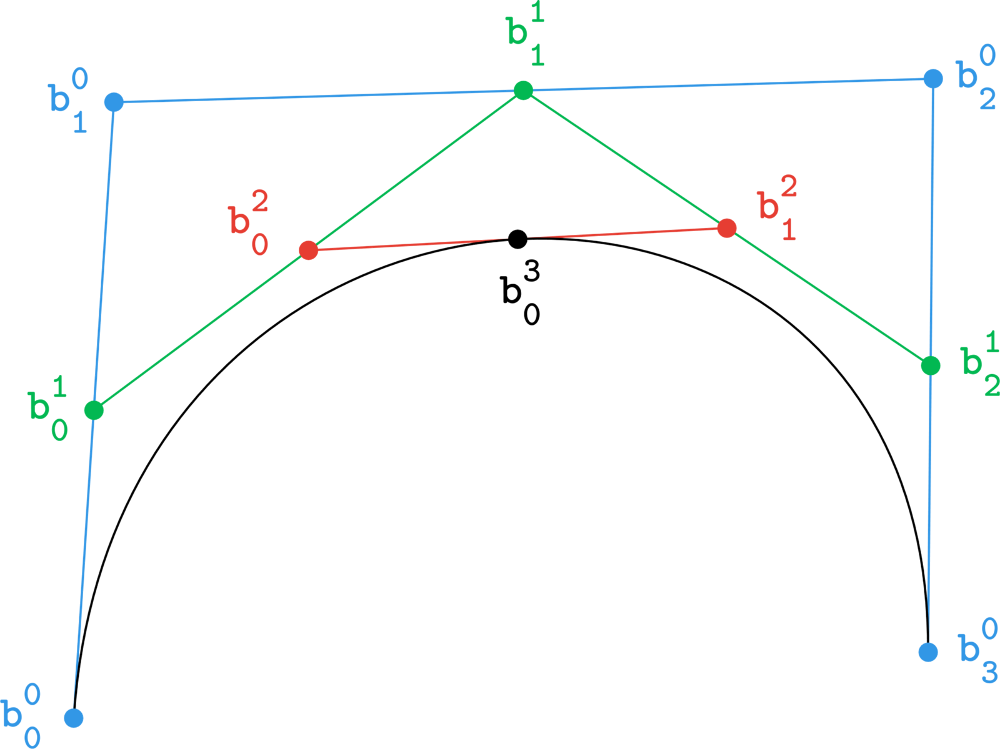
Visualisation of the steps of the De Casteljau's algorithm

Visualisation of the steps of the De Casteljau’s algorithm, $t=0.5$.

The De Casteljau’s algorithm provides an efficient means for evaluating a Bézier curve $\mathbf{x}(t)$. It is useful to look at this algorithm in its schematic form. For a quartic curve ($n=4$):

\[\begin{array}{ccccccccc} \mathbf b_0 = \mathbf b_0^0 & & & & & & & & \\ & \ddots & & & & & & & \\ \mathbf b_1 = \mathbf b_1^0 & \dots & \mathbf b_0^1 & & & & & & \\ & \ddots & & \ddots & & & & & \\ \mathbf b_2 = \mathbf b_2^0 & \dots & \mathbf b_1^1 & \dots & \mathbf b_0^2 & & & & \\ & \ddots & & \ddots & & \ddots & & & \\ \mathbf b_3 = \mathbf b_3^0 & \dots & \mathbf b_2^1 & \dots & \mathbf b_1^2 & \dots & \mathbf b_0^3 & & \\ & \ddots & & \ddots & & \ddots & & \ddots & \\ \mathbf b_4 = \mathbf b_4^0 & \dots & \mathbf b_3^1 & \dots & \mathbf b_2^2 & \dots & \mathbf b_1^3 & \dots & \mathbf b_0^4 = \mathbf x(t) \end{array}\]

Animation of the De Casteljau's algorithm for a quintic curve

Animation of the De Casteljau’s algorithm for a quintic curve ($n=5$).

Code

git clone https://github.com/bbrrck/geo-num-2016.git
cd geo-num-2016/TP1
mkdir build
cd build
cmake ..
make
./geonum_TP1

For rendering, you can use gnuplot or matplotlib. While still in the build/ directory, test them by running :

gnuplot -p ../plots/plot.gnu
python ../plots/plot.py

Many of you have reported problems with gnuplot due to the line set terminal qt. Change it to something else to make things work, e.g. set terminal x11. For a complete list of terminals available on your machine, execute

echo "set terminal" | gnuplot

ToDo

~~Implement the computation of a curve point $\mathbf x(t)$ using Bernstein polynomials.~~
Implement the De Casteljau algorithm for a parameter $t$.
Evaluate the curve using ~~both methods and compare their performance~~ the De Casteljau algorithm for various sampling densities.
Visualise the curve and its Bézier polygon. Use all input files from the data/ folder.
Visualise the intermediate polygons $\mathbf b_i^k$ from the De Casteljau algorithm for a fixed parameter $t$. (Only the simple.bcv is enough.)

Resources