TP9 : Subdivision Surfaces on Triangle Meshes
Code
As always, do
git pull
or, if you don’t have the local repo,
git clone https://github.com/bbrrck/geo-num-2016.git
Then
cd TP9/
mkdir build
cd build
cmake ..
make
./geonum_TP9 sphere
Later, you can specify number of subdivision steps via additional command line parameter.
./geonum_TP9 sphere 3
SimpleViewer controls are listed below (should be the same on AZERTY keyboard).
face toggle : F
edge toggle : E
light on/off : L
smooth/flat : S
zoom : (mouse scroll) or [pageup]/[pagedown]
rotate : (mouse click & drag)
Important: For those still having problems with SimpleViewer, a code with python binding to OpenGL is provided.
More info on how to configure everything is at the end of the text.
Subdivision surfaces
Mesh subdivision is a powerful tool, extensively used in modern geometric modeling. Unlike B-spline subdivision you implemented in TP8, subdivision surfaces are not limited to rectangular topology; in fact they provide the means for representing surfaces of arbitrary topology.
Almost every current animated movie uses subdivision surfaces to some extent. Even though their mathematical foundations date back to 1978, Pixar’s short Geri’s Game (1997) is considered to be the first ‘real’ application.


Geri’s game, an Academy award-winning short movie by Pixar.
Loop subdivision scheme
Today, you’ll be implementing the Loop subdivision scheme for triangle meshes. Like every surface subdivision scheme, it consists of two general steps:
- Split the topology; each triangle is replaced by four smaller triangles.
- Compute the new vertex positions from the old positions.
The first step is already provided in the code; only the second part needs to be implemented.
To compute the new geometry, two sets of vertices are recognized, each with its own rules: new edge midpoints and old vertices. The masks for both groups are visualised below.
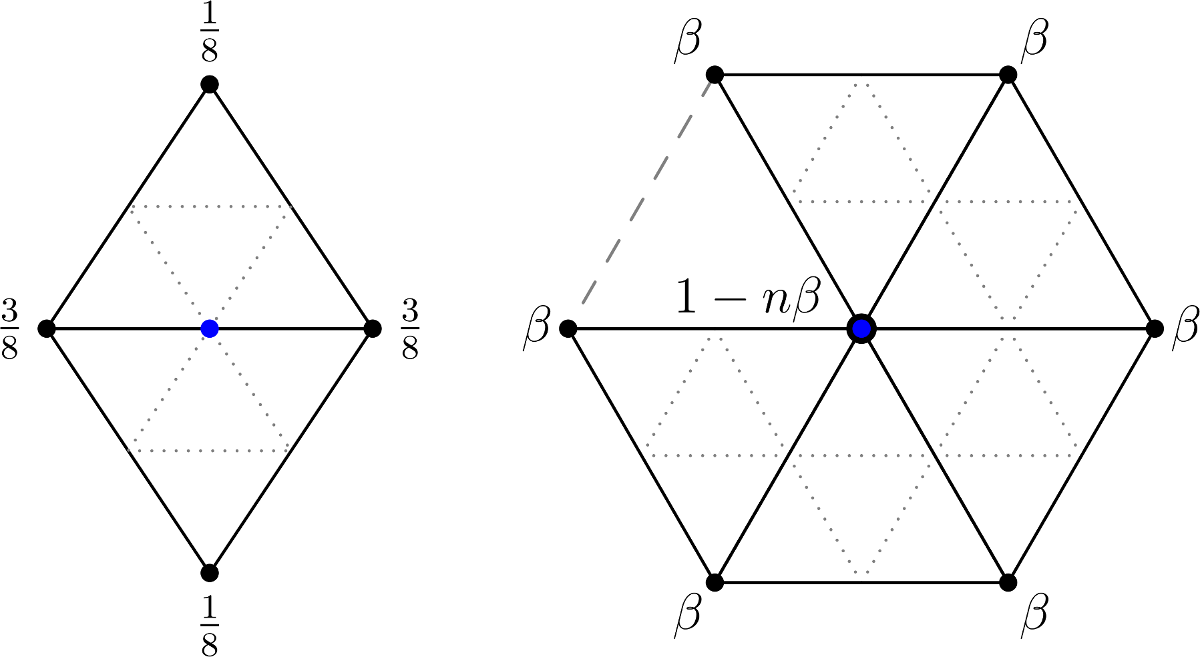
Edge and vertex masks for the Loop subdivision scheme.
The $n$ in the vertex mask denotes the number of neighbours. The original definition of $\beta$ was introduced by Charles Loop in his master’s thesis (1987):
\[\beta = \frac1{n} \left( \frac58 - \left( \frac38 + \frac14 \cos{\frac{2\pi}{n}} \right)^2 \right)\]Joe Warren proposed using the simplified weights (1995):
\[\beta = \begin{cases} \frac{3}{8n} & n > 3, \\ \frac{3}{16} & n = 3 . \end{cases}\]Implementation
To represent a triangle mesh with arbitrary topology, we use two matrices.
- geometry
V—V.row(i)is the position of the vertexi. - topology
F—F.row(j)are the indices of three vertices in trianglej.
Example: sphere
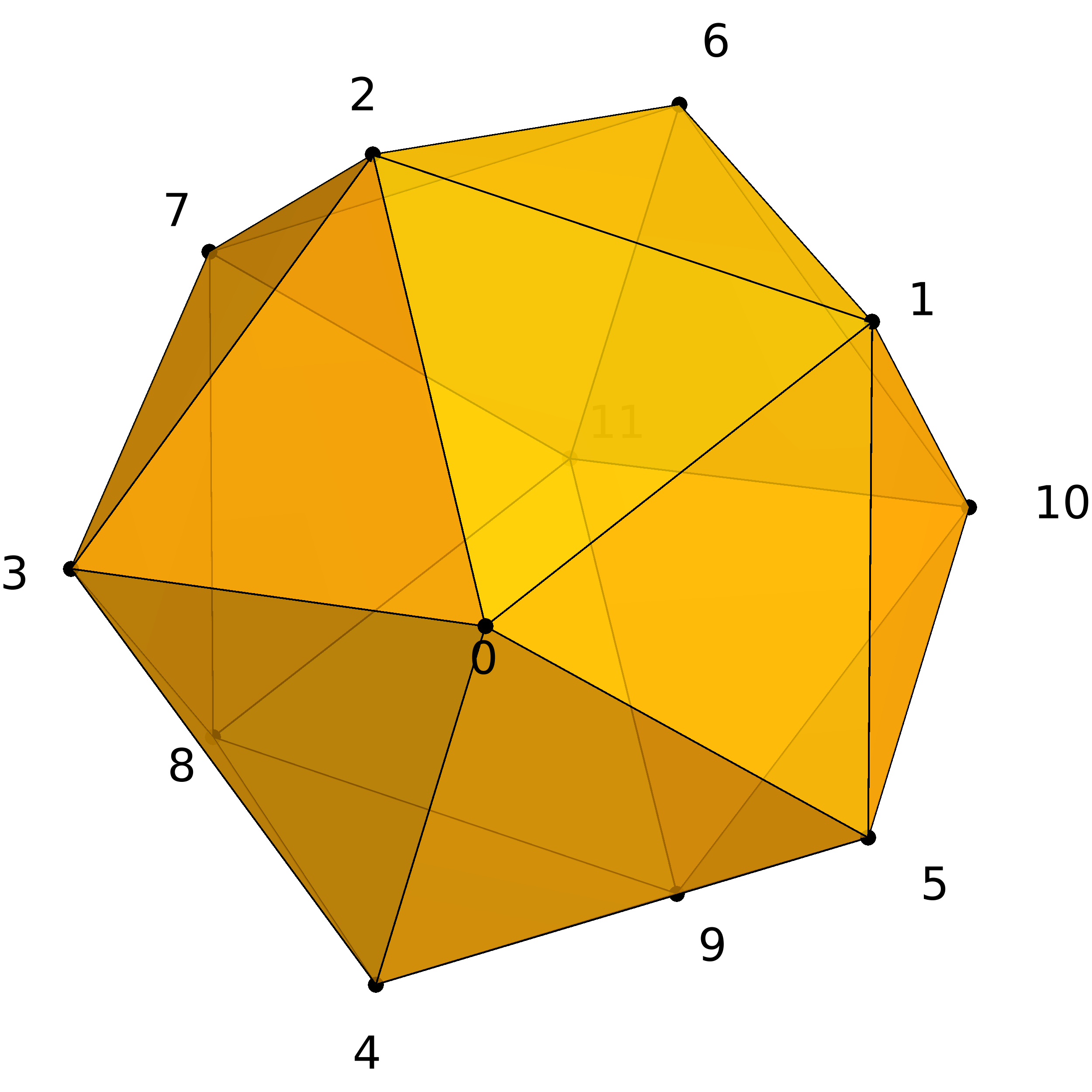
Adjacency
The topological step is implemented in the function triangleSplit( F0,V0, F1,V1, VertexAdjacency, MidpointAdjacency );.
After the execution of this function, the last two arguments contain indices necessary to compute the new geometry.
If v, e is the number of vertices and edges in the mesh V0, F0, then
VertexAdjacencyis a matrix with v rows, row i contains adjacency information for old vertex i.
column 0: number of adjacent vertices = $n$
columns 1-n: indices of adjacent vertices (weight $\beta$)MidpointAdjacencyis a matrix with e rows, row j contains adjacency information for new midpoint vertex j.
columns 0 and 1: indices of adjacent edge vertices (weight $\frac38$)
columns 2 and 3: indices of opposite vertices (weight $\frac18$)
ToDo
- Implement the computation of new geometry in the Loop subdivision scheme using the original weights $\beta$.
- Use the simplified weights (Warren) and compare the results.
- Subdivide the sphere and cube five times. Which surface is closer to the real sphere? Why?
Test surfaces
This is the list of all provided test surfaces, with vertex and face counts.
Don’t apply too many iterations on surfaces with more faces, as the number of faces grows exponentially. Take the horse mesh with 1000 faces for instance: we get 4000 faces after one iteration, 16000 after two, and 64000 after three.
In general, three iterations are sufficient. For the sphere and cube, up to five iterations should work. If you get a failed assertion somewhere, it probably means there are too many vertices in the mesh.
| #V | #F | |
|---|---|---|
| cube | 8 | 12 |
| sphere | 12 | 20 |
| testsurf | 69 | 134 |
| bumpycube | 201 | 398 |
| cow | 278 | 552 |
| armadillo | 434 | 864 |
| horse | 502 | 1000 |
Resources
- Pixar’s OpenSubdiv
- A Quick Introduction to Subdivision Surfaces by Ryan Holmes
- Subdivision by Matthew Fischer
- behind the scenes video showing the use of subdivision surfaces in Brave
Appendix: PyOpenGL
Here are the instructions on how to configure PyOpenGL and use the python script viewsurface.py
based on the code by Matthijs Douze.
Modify the configuration as needed. Be sure to use absolute paths!
curl -O https://pypi.python.org/packages/source/P/PyOpenGL/PyOpenGL-3.1.0b3.tar.gz
tar xvzf PyOpenGL-3.1.0b3.tar.gz
cd PyOpenGL-3.1.0b3
mkdir -p /home/tibor/TP-geo-num/TP9/plots/lib/python2.7/site-packages/
export PYTHONPATH=/home/tibor/TP-geo-num/TP9/plots/lib/python2.7/site-packages/
python setup.py install --prefix=/home/tibor/TP-geo-num/TP9/plots
cd /home/tibor/TP-geo-num/TP9/plots
python viewsurface.py sphere
This assumes you already have an exported sphere.off in your plots folder.
You can also test using the input data:
python viewsurface.py ../data/sphere
Don’t forget to use cmake/CMakeLists2.txt and to comment the lines 2, 61-65 in main.cpp.