TP5 : Uniform B-splines as Subvidision Curves
Code
Do
git pull
or, if you don’t have the local repo,
git clone https://github.com/bbrrck/geo-num-2016.git
As usual, test by
cd TP5/
mkdir build
cd build
cmake ..
make
./geonum_TP5 simple
Uniform B-splines
In TP3, you have implemented the De Boor’s algorithm for evaluation of general B-splines. Now, let’s have a look at a particular subclass of B-spline curves, characterized by the uniform knot vector $t_i = i \; \; \forall i \in \mathbb Z$; have a look at the basis induced by such vector.
Your today’s task will be to implement these uniform B-splines as subdivision curves.
Subdivision algorithm
For a given degree $k$, the following constitutes one subdivision step passing from a polygon with $p$ points $\left\lbrace x_i^n \right\rbrace_{i=0}^{p-1}$ to a polygon with $2p$ points $\left\lbrace x_i^{n+1} \right\rbrace_{i=0}^{2p-1}$.
Double the points :
\[d_{2i}^0 = x_i^n, \quad d_{2i+1}^0 = x_i^n \quad \text{for} \quad i=0,\dots,p-1\]Average $k$ times :
\[d_i^j = \frac12 \left( d_i^{j-1} + d_{i+1}^{j-1} \right) \quad \text{for} \quad j=1,\dots,k\]Replace :
\[x_i^{n+1} = d_i^k \quad \text{for} \quad i=0,\dots,2p-1\]This procedure is sometimes refered to as the Lane–Riesenfeld algorithm.
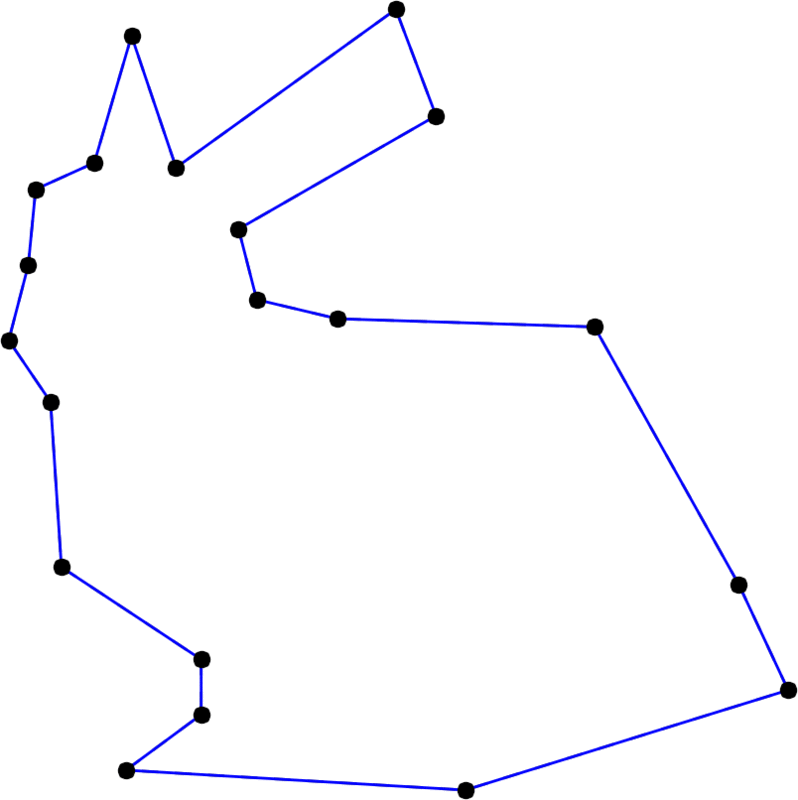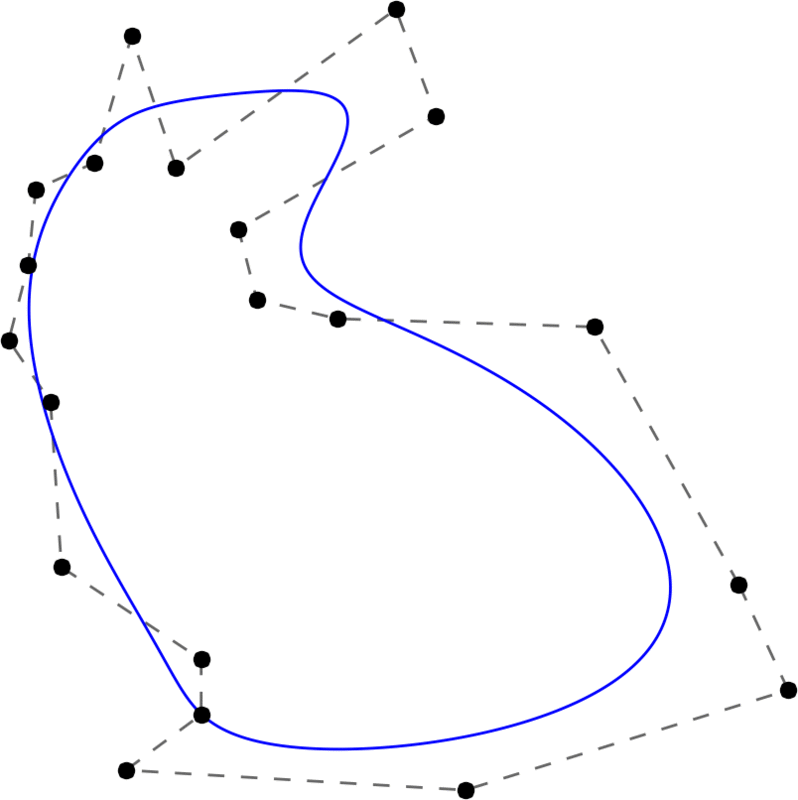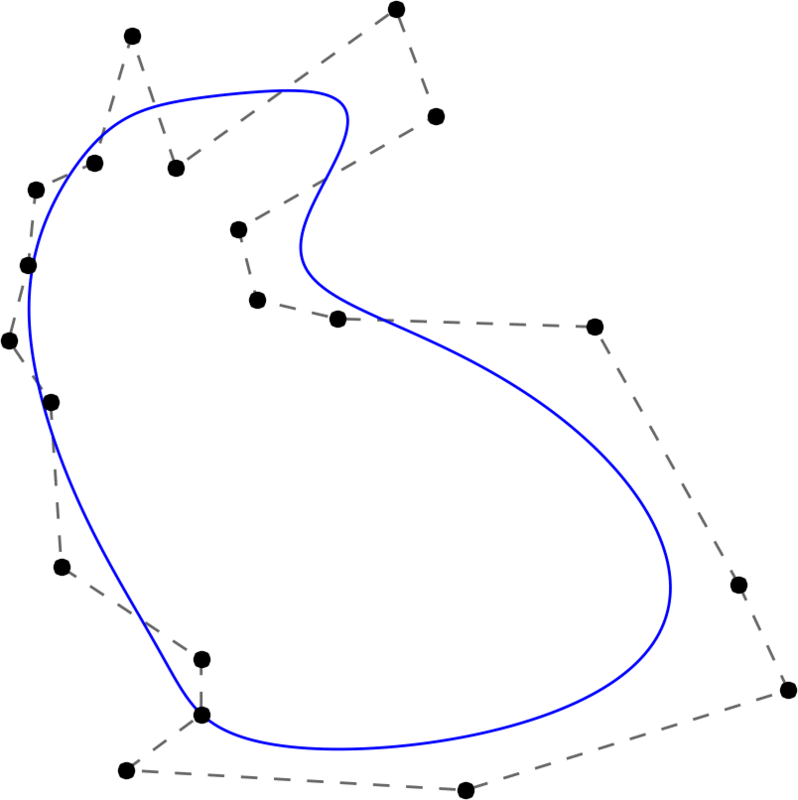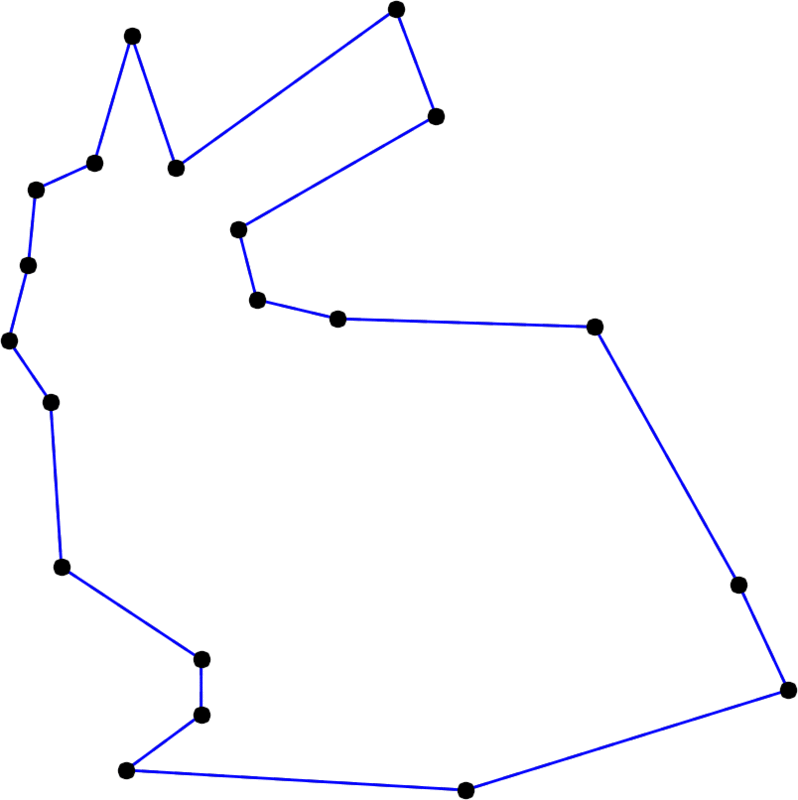
With increasing degree, the Stanford bunny becomes smoother and smoother. Here, the degree runs from 2 to 20 and back.
ToDo
- Implement the subdivision algorithm for (closed) uniform B-spline curves. Test with various values of the degree $k$.
- Simplify the scheme for $k=2$. What do you observe?
Resources
- Subdivision curves on Numerical Tours by Gabriel Peyré
- Subdivision spline curves