TP4 : Subdivision curves
Code
Do
git pull
or, if you don’t have the local repo,
git clone https://github.com/bbrrck/geo-num-2016.git
As usual, test by
cd TP4/
mkdir build
cd build
cmake ..
make
./geonum_TP4 simple
Subdivision Curves
A subdivision curve is defined as the limit of recursive refinement of the input polyline $\mathbf x_i = \mathbf x_i^0$. Your today’s task is to implement three curve subdivision schemes from the lecture. For the sake of simplicity, we will be working with closed curves only.
Chaikin
\[\left\lbrace \begin{align} \mathbf x_{2i }^{k+1} & = \tfrac34 \mathbf x_i^k + \tfrac14 \mathbf x_{i+1}^k \\ \mathbf x_{2i+1}^{k+1} & = \tfrac14 \mathbf x_i^k + \tfrac34 \mathbf x_{i+1}^k \end{align} \right.\]Corner-cutting
$ 0 < a < b < 1 $ :
\[\left\lbrace \begin{align} \mathbf x_{2i }^{k+1} & = (1-a) \mathbf x_i^k + a \mathbf x_{i+1}^k \\ \mathbf x_{2i+1}^{k+1} & = (1-b) \mathbf x_i^k + b \mathbf x_{i+1}^k \end{align} \right.\]Four-point scheme
\[\left\lbrace \begin{align} \mathbf x_{2i }^{k+1} & = \mathbf x_i^k \\ \mathbf x_{2i+1}^{k+1} & = \tfrac1{16} \left( - \mathbf x_{i-1}^k + 9 \mathbf x_{i}^k + 9 \mathbf x_{i+1}^k - \mathbf x_{i+2}^k \right) \end{align} \right.\]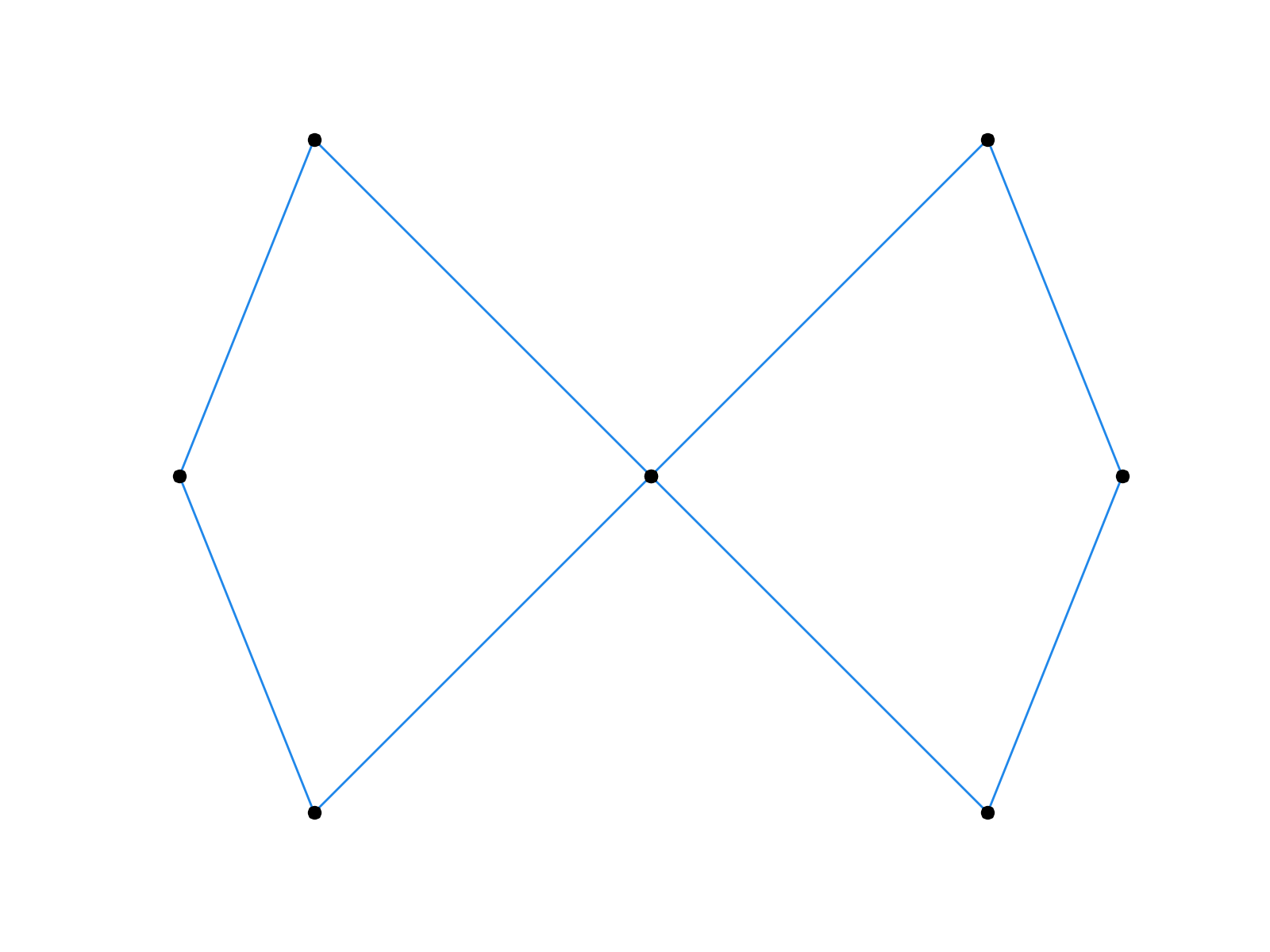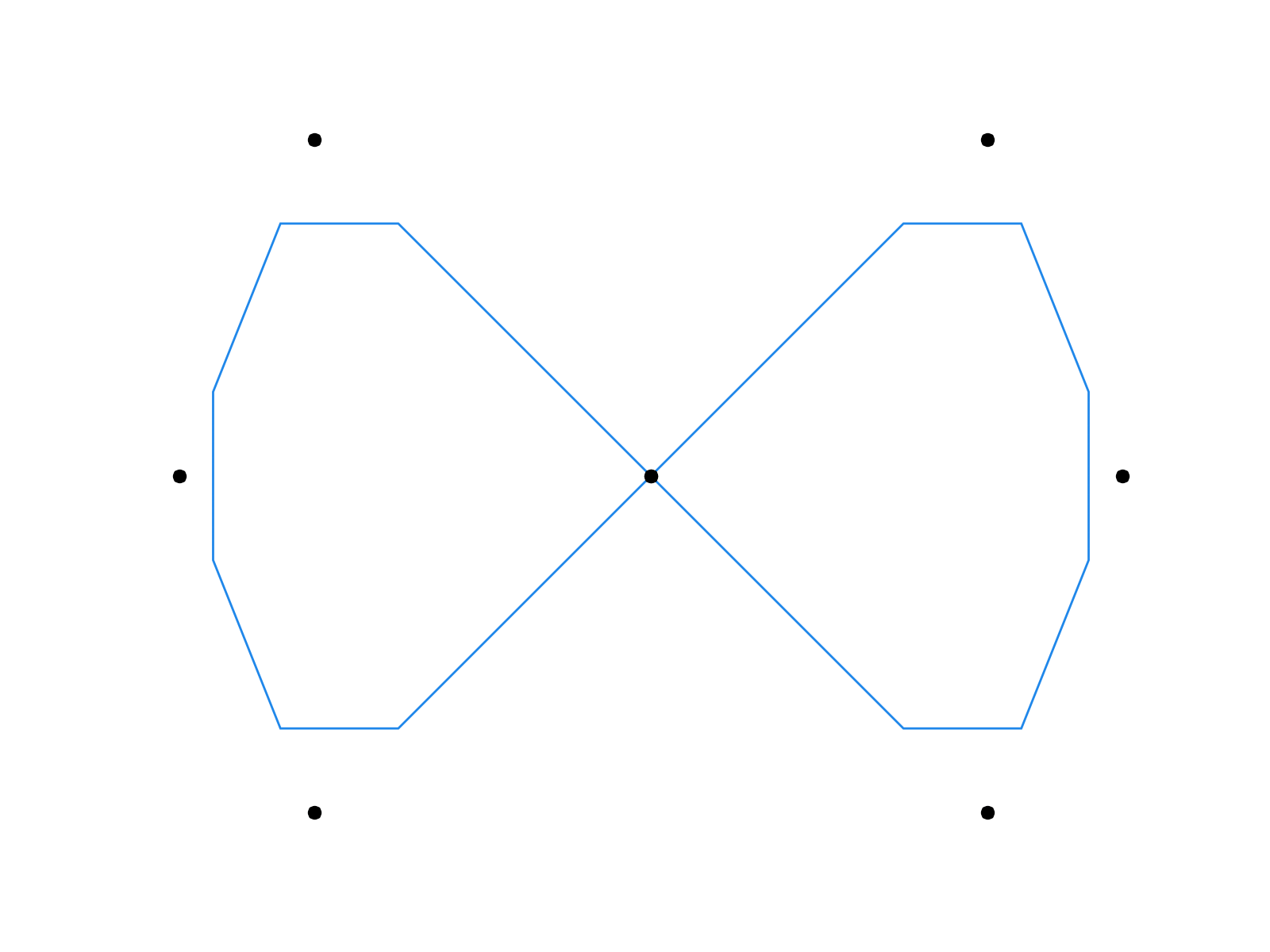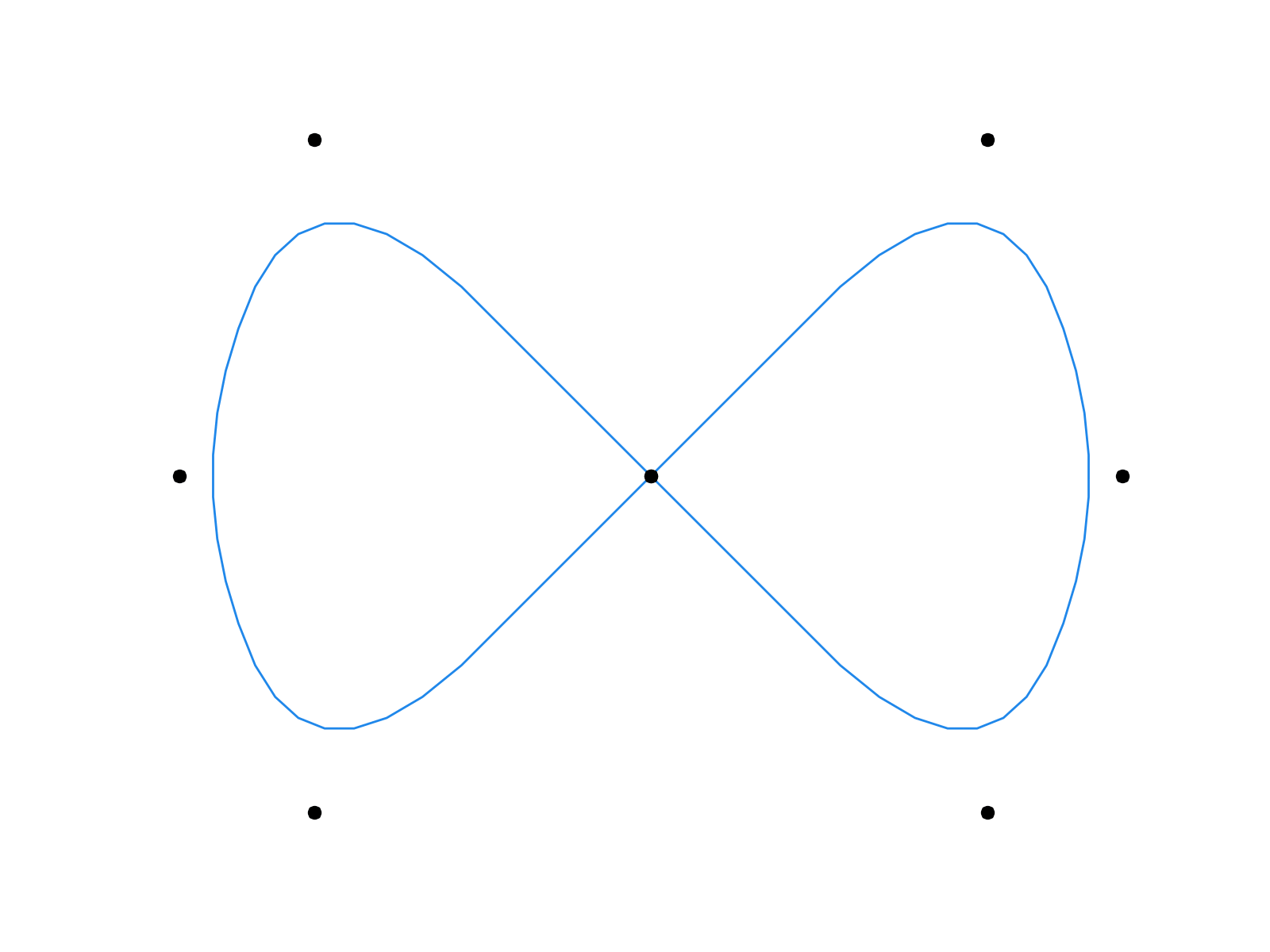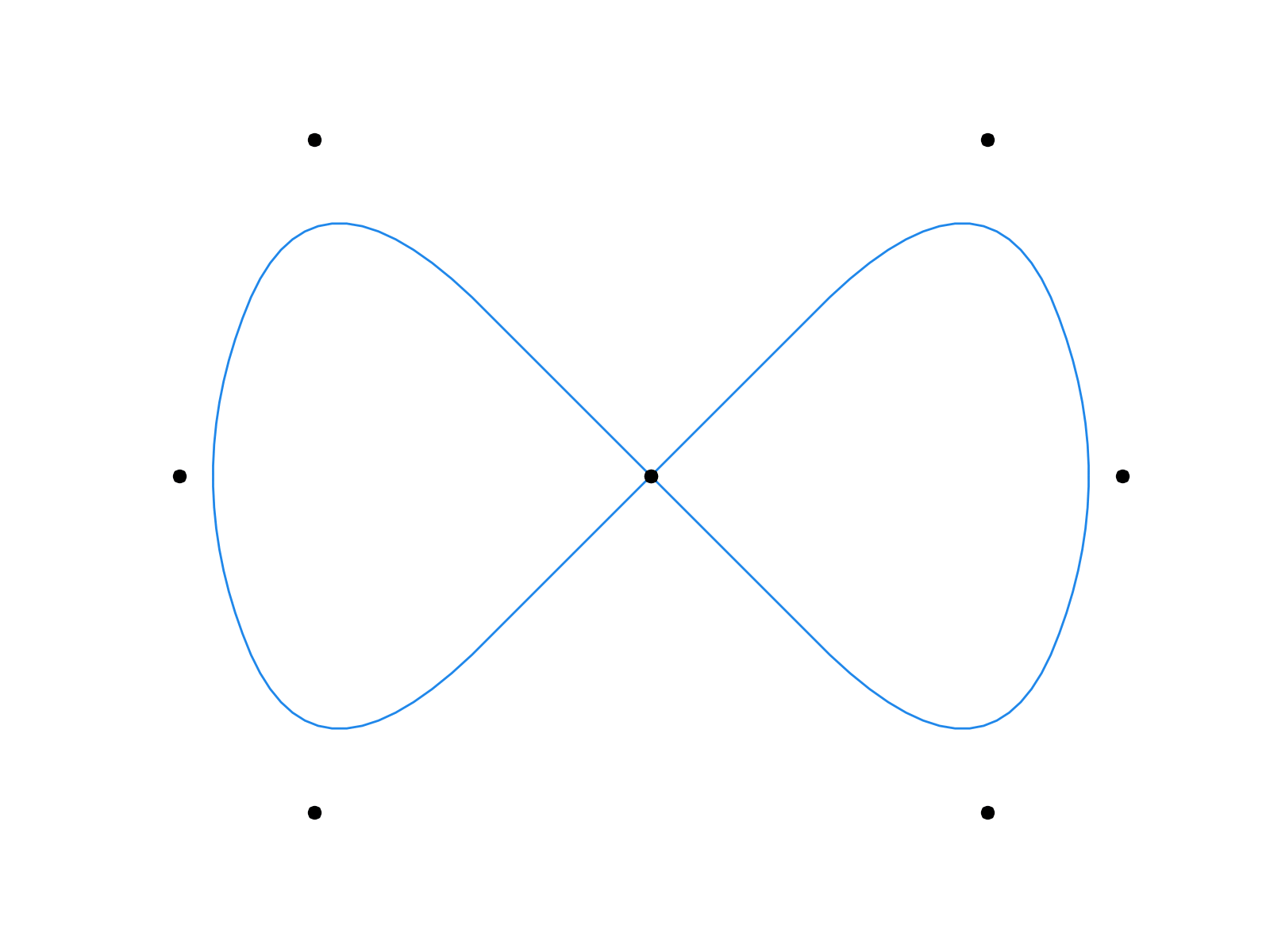
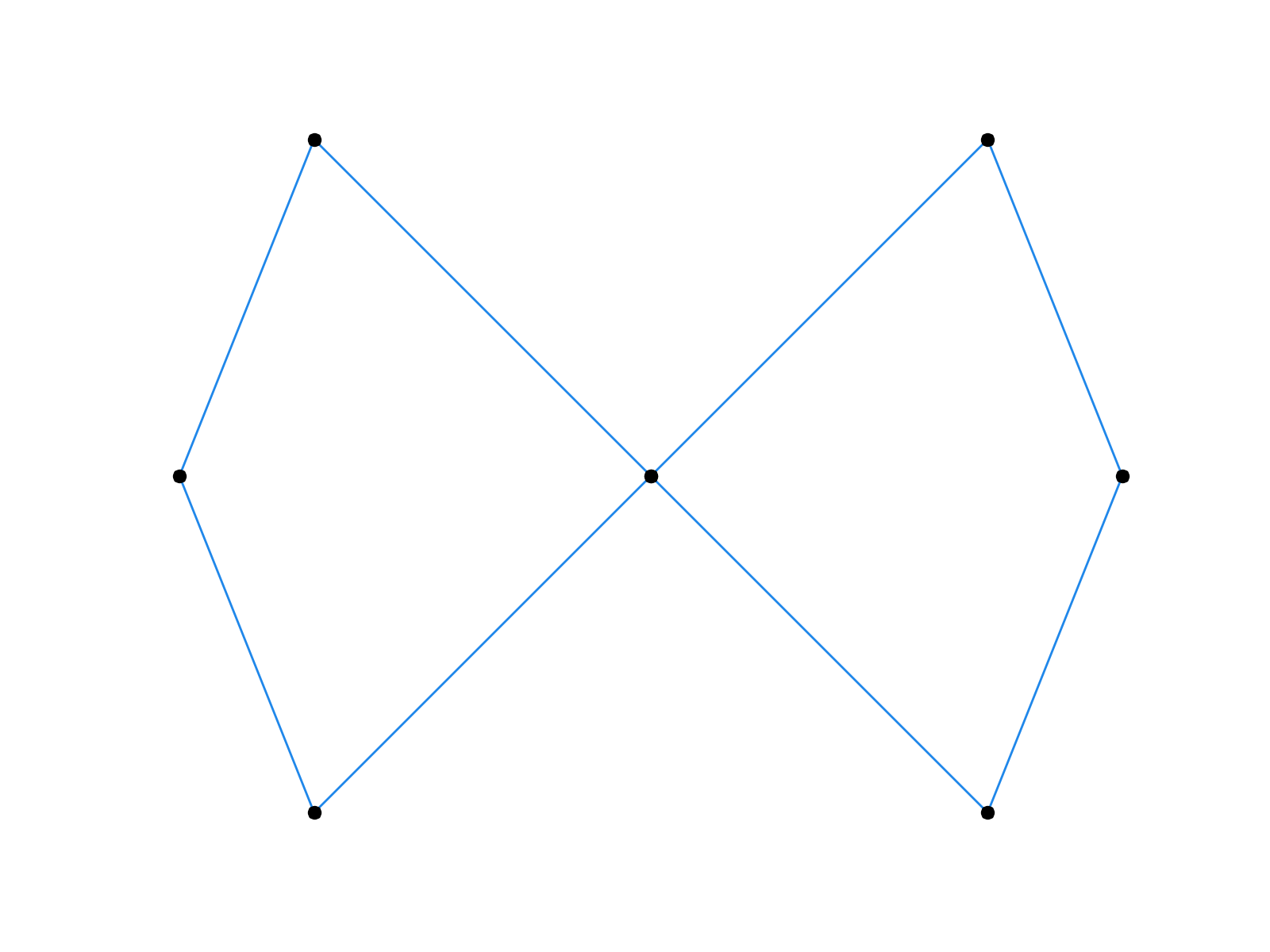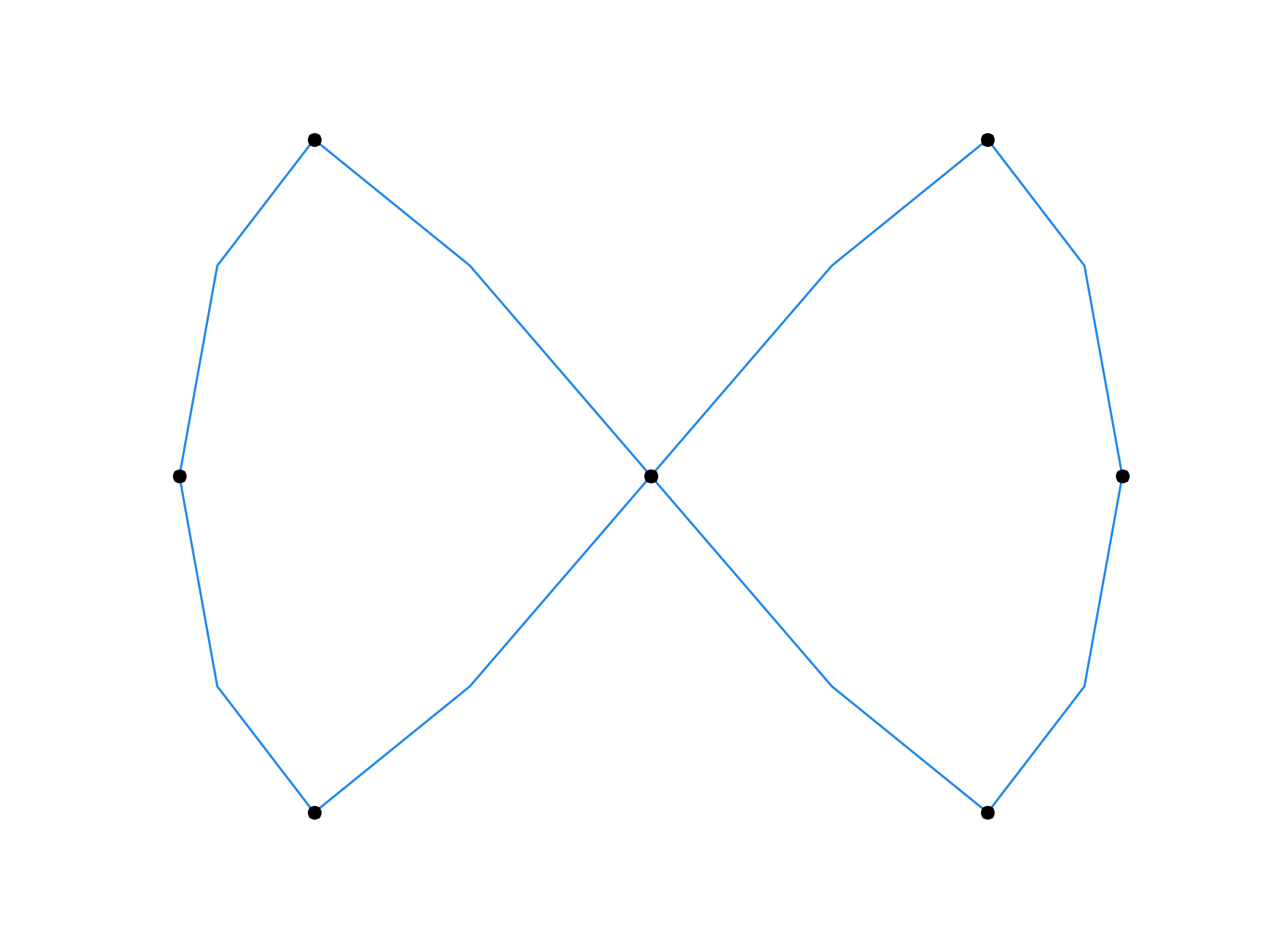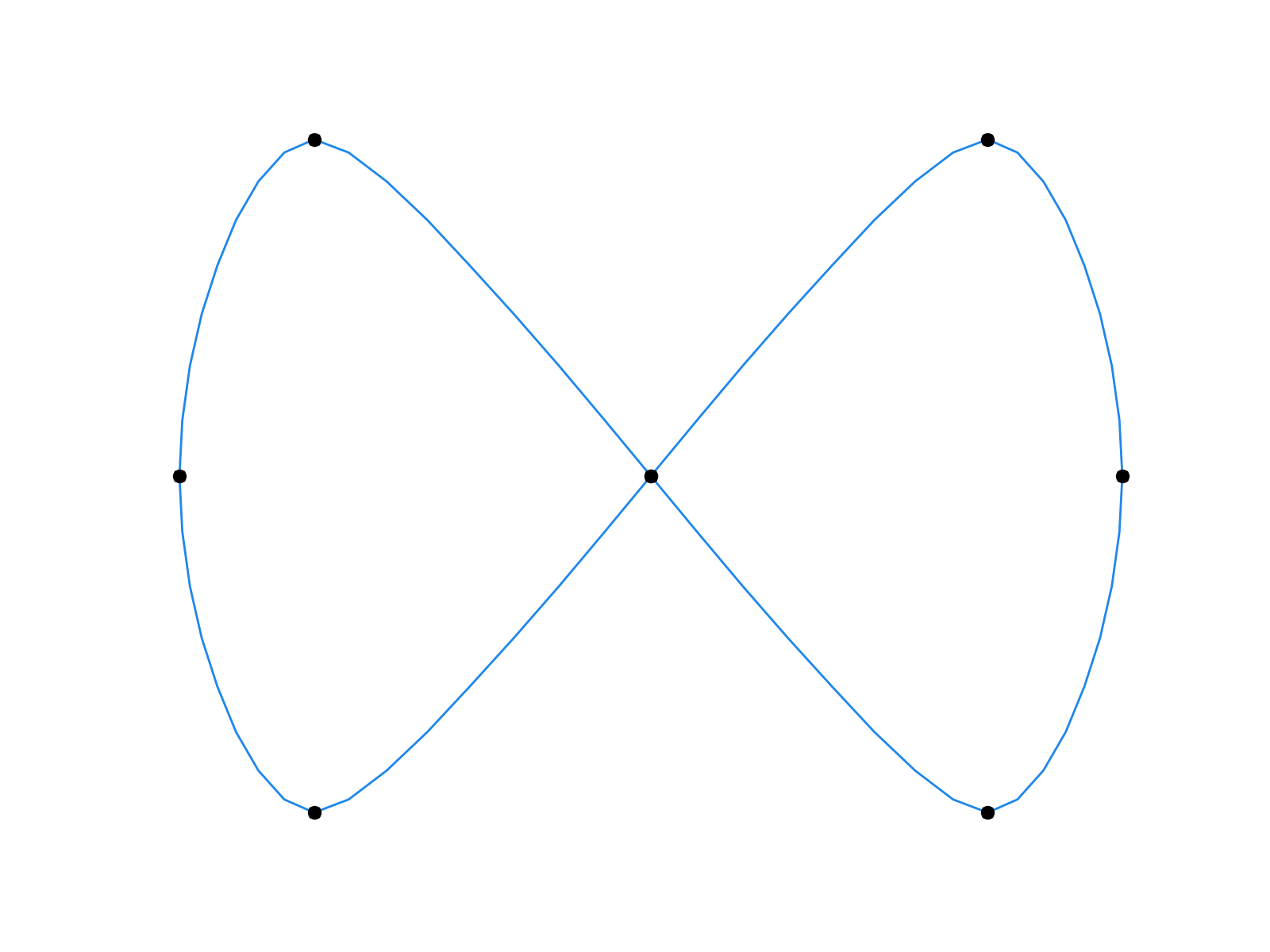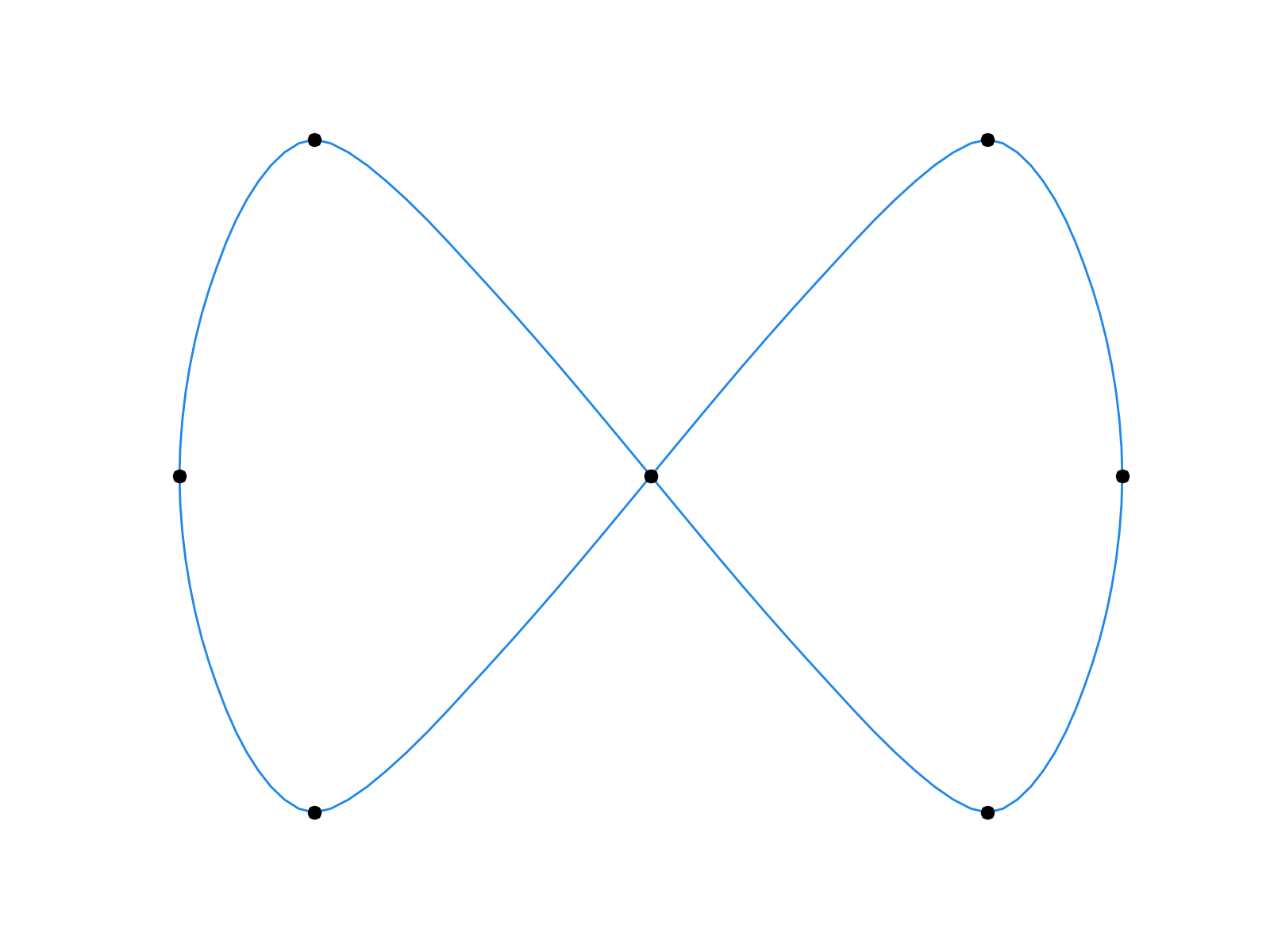
First few iterations of the Chaikin’s algorithm (left) and the four-point scheme (right).
ToDo
- Implement the three subdivision schemes (for closed curves only).
Test your implementation on the
simpleandinfinitydatasets. To visualise:
python ../plots/plot.py simple|infinity - Experiment with different values of $a,b$ in corner cutting. Specifically, try using
- $b=a+\frac12$
- $b \neq a+\frac12$
What do you observe?
- (bonus) A generalized four-point scheme uses the mask $[-\omega,\frac12+\omega,\frac12+\omega,-\omega].$ The above version of the algorithm uses $\omega=\frac1{16}.$ Modify your implementation of this algorithm to account for the tension parameter $\omega$ and try varying its value. You should get $\mathcal C^1$ limit curves for $\omega \in \left[0,(\sqrt 5 - 1)/8 \approx 0.154 \right]$.
Resources
- Subdivision curves on Numerical Tours by Gabriel Peyré
- Lecture on subdivision curves by Don Fussell