TP8 : Uniform B-splines as Subdivision Surfaces
Code
Do
git pull
or, if you don’t have the local repo,
git clone https://github.com/bbrrck/geo-num-2016.git
As usual, test by
cd TP8/
mkdir build
cd build
cmake ..
make
./geonum_TP8 torus
If everything goes well, you should see a cube. The viewer can be controlled with the mouse: click and drag to rotate, scroll to zoom (also works with pageup/pagedown keys), press W to toggle the wireframe mode (or Z on AZERTY keyboard).
In case the SimpleViewer does not work, you can still export and visualise the surfaces via the python script, included in plots/.
Algorithm
Much like in the curve case (recall Chaikin in TP4 or Lane-Riesenfeld in TP5), a uniform bi-quadratic B-spline surface ($k=2,l=2$) can be evaluated by iterative subdivision of the initial control net $V^0_{i,\;j}$. Here’s the algorithm to perform one step of the subdivision.
At the $k$-th iteration, for each cell of the grid composed of the vertices $V^k_{i,\;j}$ $V^k_{i+1,\;j}$ $V^k_{i,\;j+1}$ $V^k_{i+1,\;j+1}$ we define a new grid as follows
\[\begin{array}{ll} V^{k+1}_{2i,\;2j} &= \frac1{16} \left( 9V^k_{i,\;j} + 3V^k_{i+1,\;j} + 3V^k_{i,\;j+1} + 1V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i+1,\;2j} &= \frac1{16} \left( 3V^k_{i,\;j} + 9V^k_{i+1,\;j} + 1V^k_{i,\;j+1} + 3V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i,\;2j+1} &= \frac1{16} \left( 3V^k_{i,\;j} + 1V^k_{i+1,\;j} + 9V^k_{i,\;j+1} + 3V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i+1,\;2j+1} &= \frac1{16} \left( 1V^k_{i,\;j} + 3V^k_{i+1,\;j} + 3V^k_{i,\;j+1} + 9V^k_{i+1,\;j+1} \right). \end{array}\]Important: If the surface is closed (cyclic) in the direction $u$, the subscripts $\scriptstyle i+1$ of $V^k$ are taken modulo the number of vertices in the direction $u$. The same applies for the direction $v$ and the subscripts $\scriptstyle j+1$.
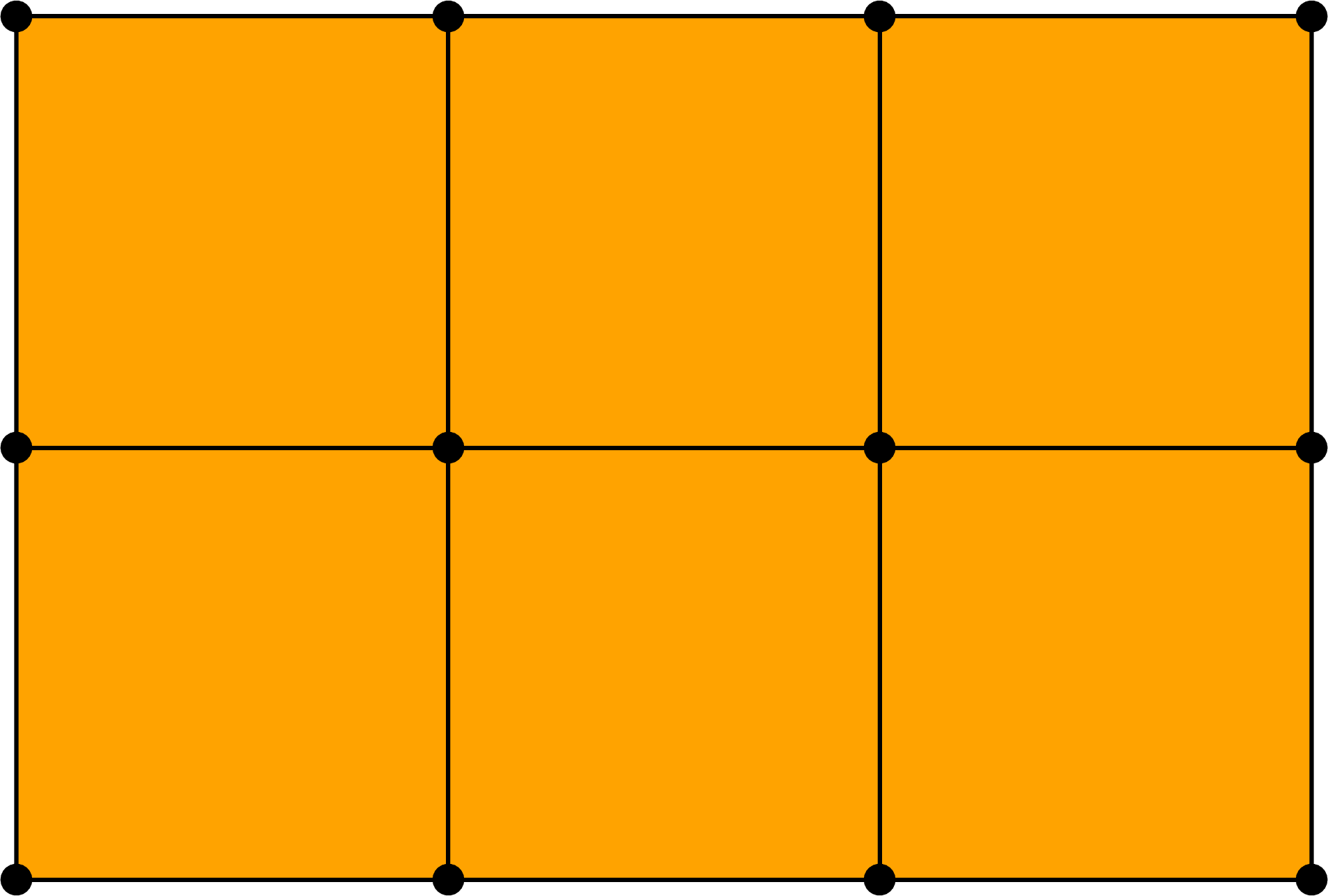
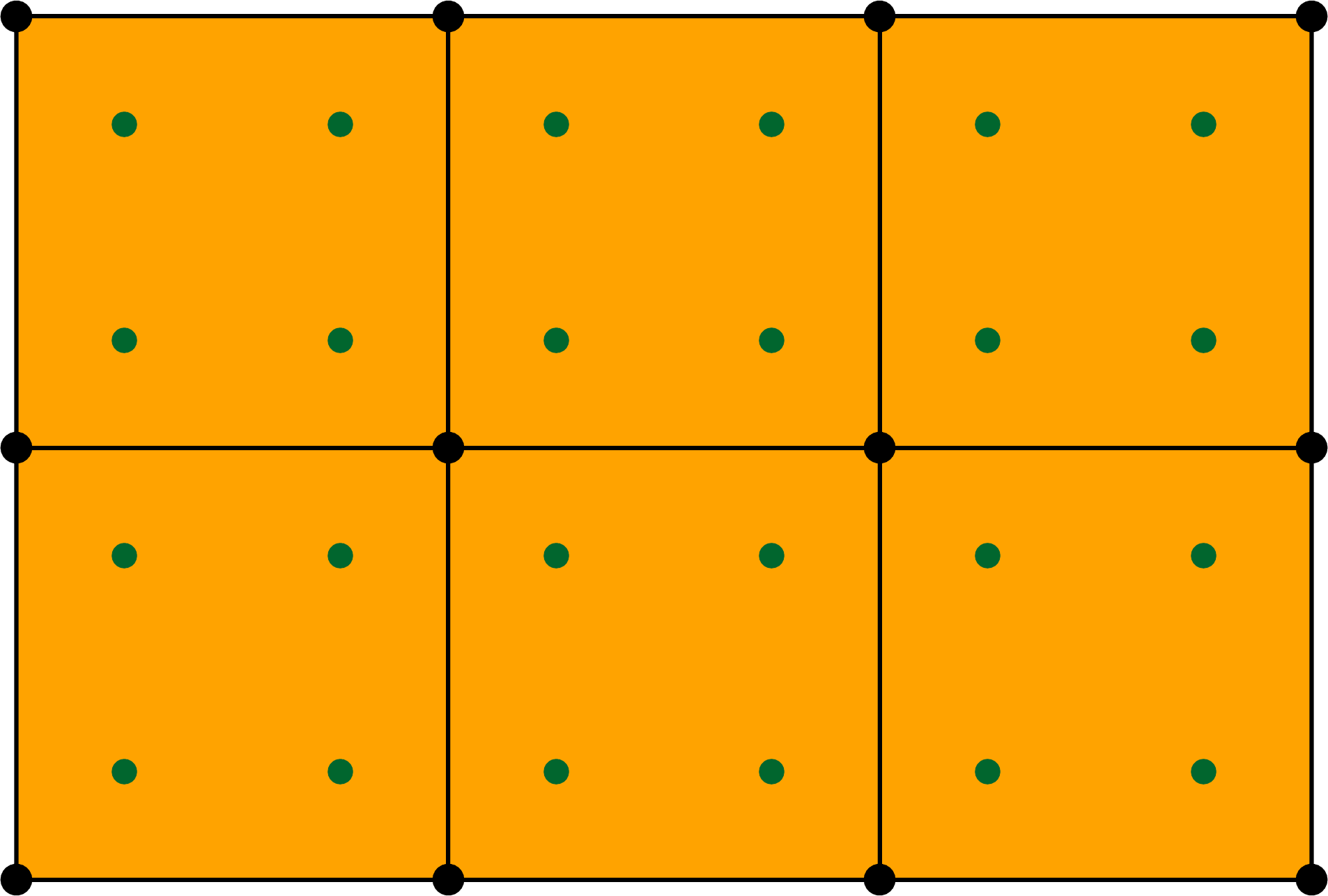
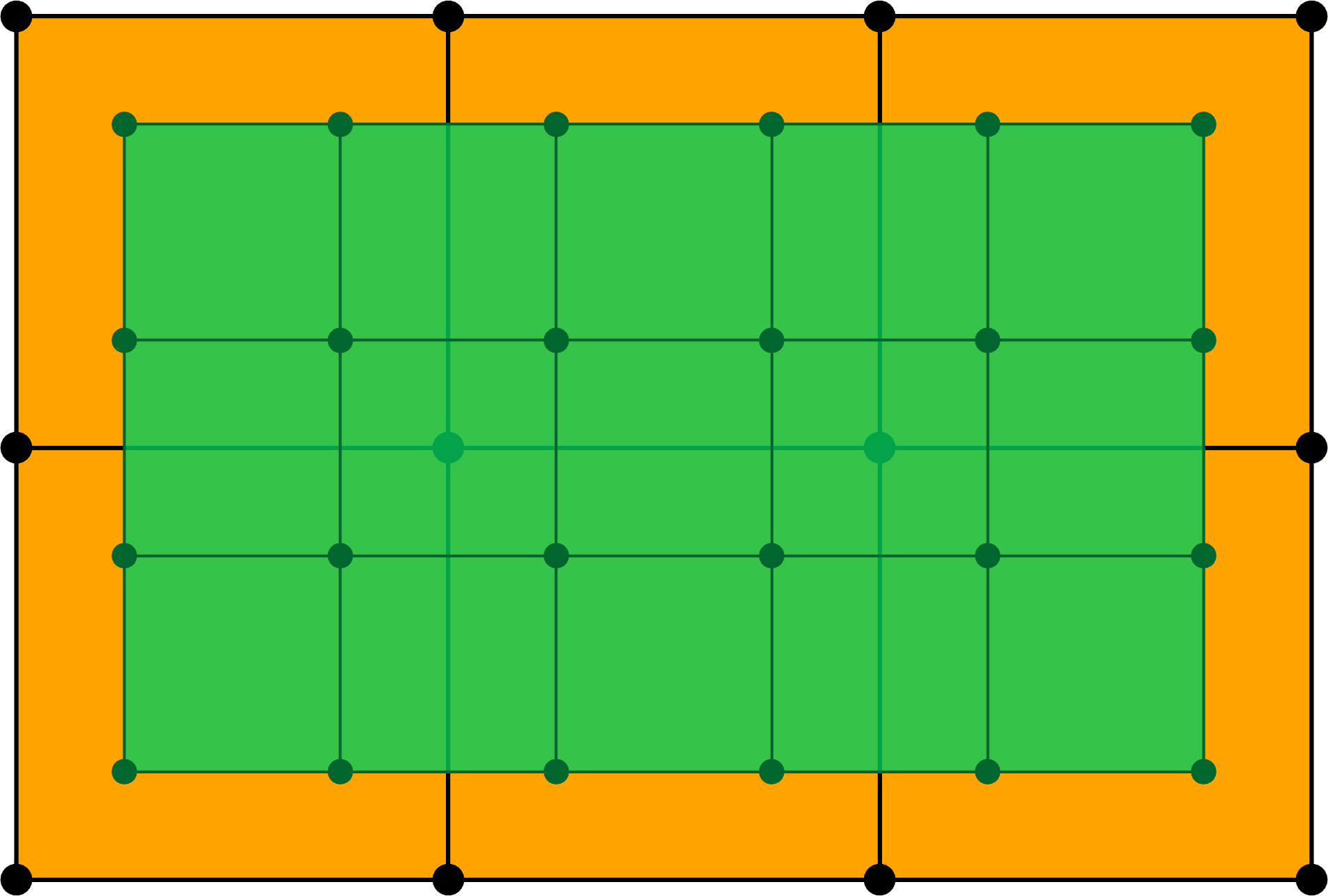
A subdivision step, open surface.
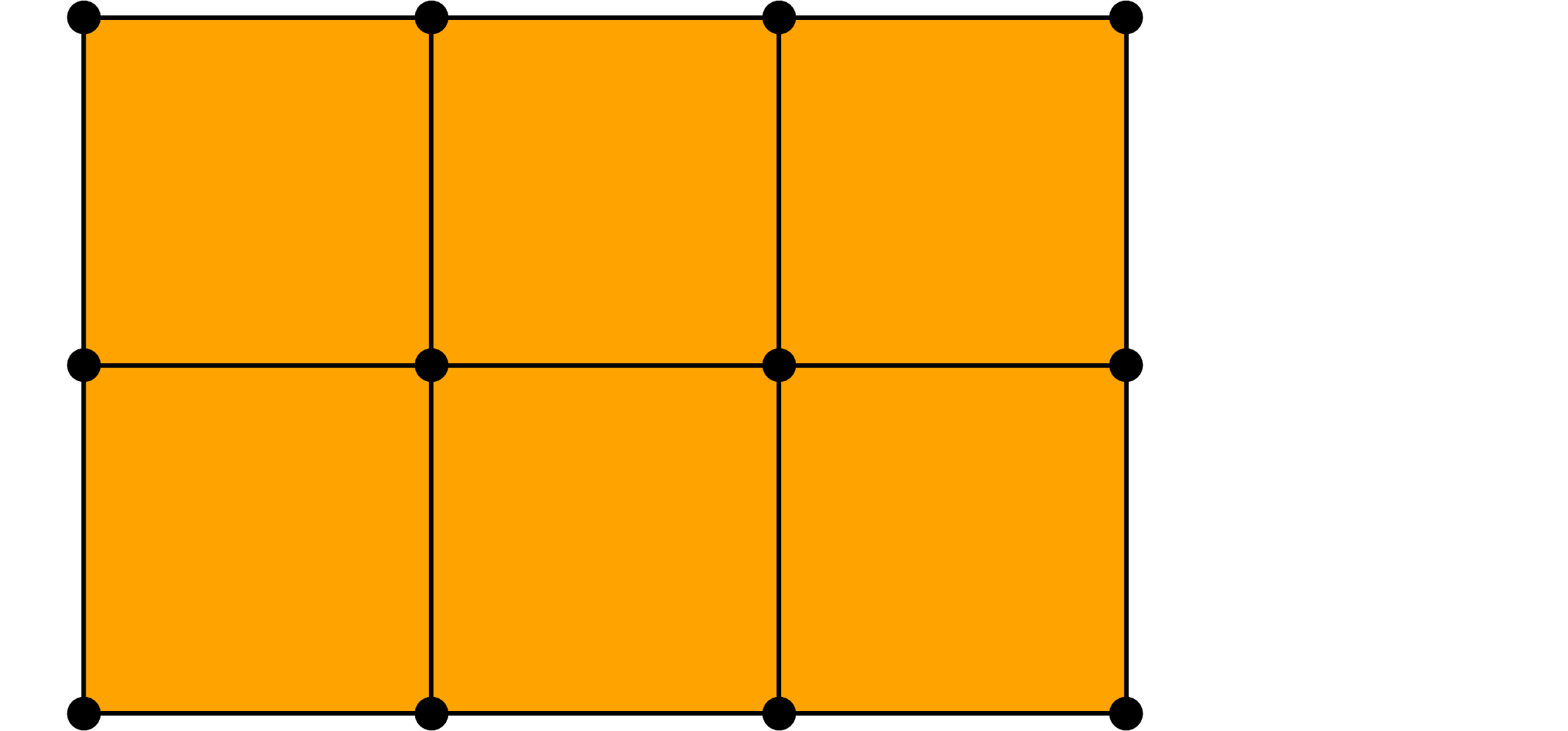
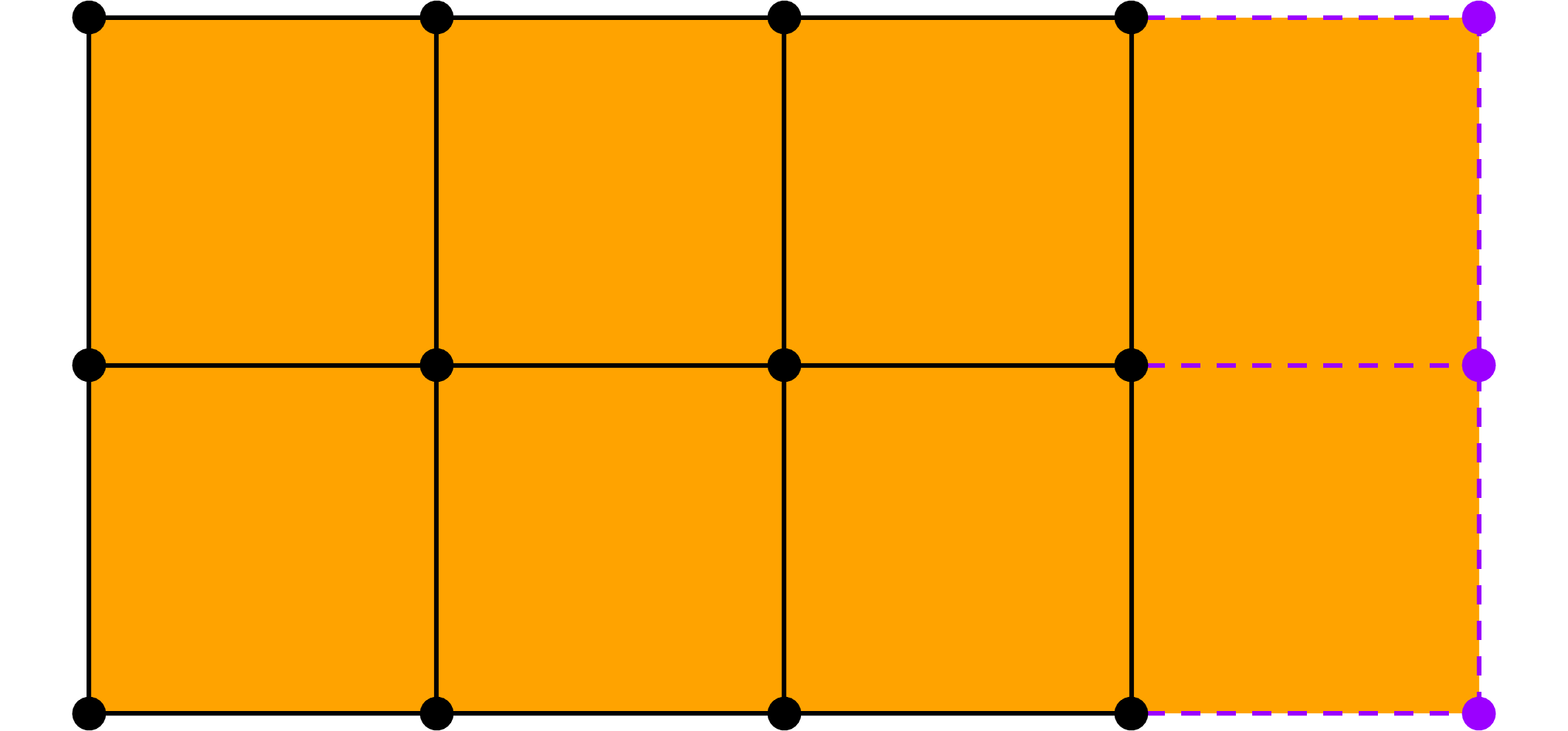

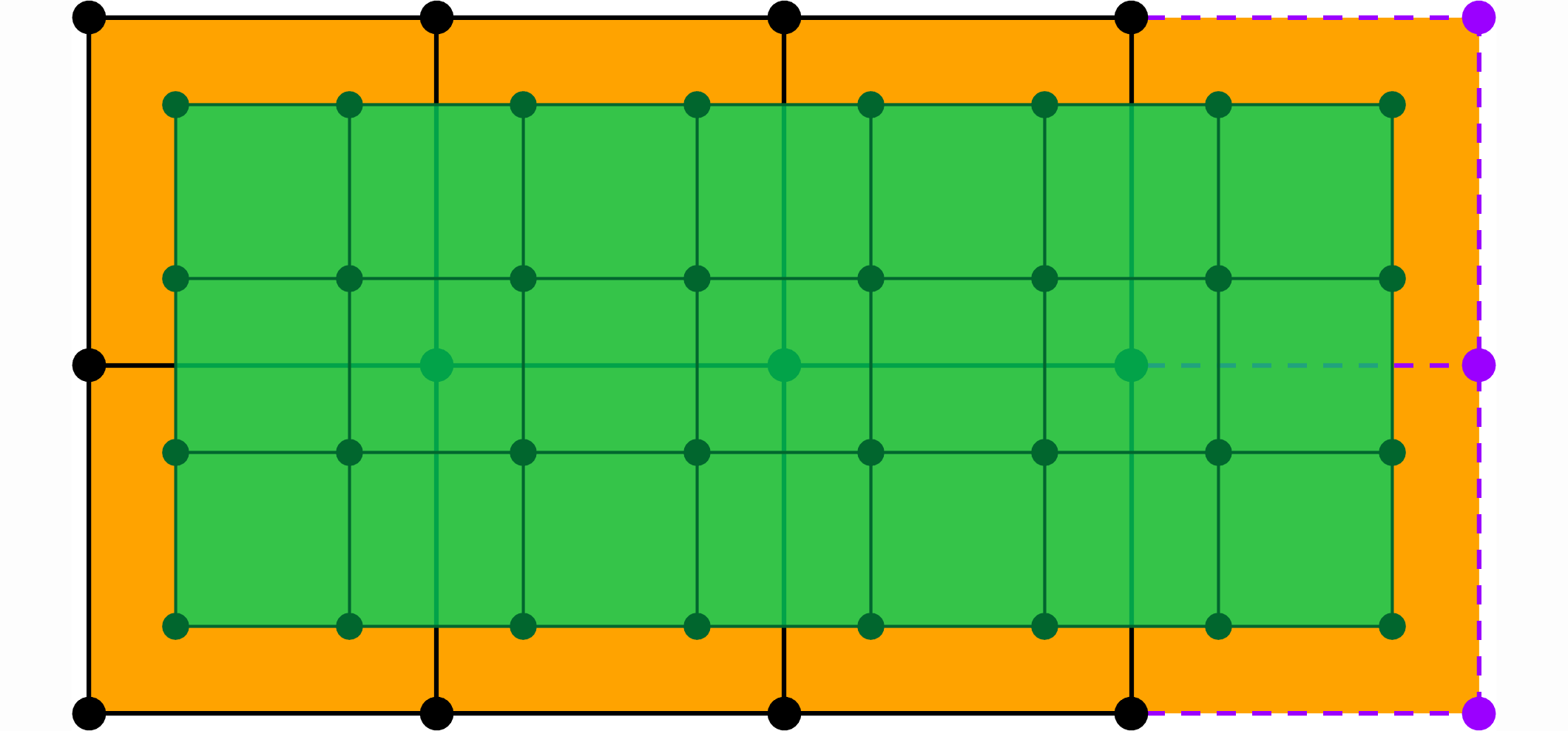
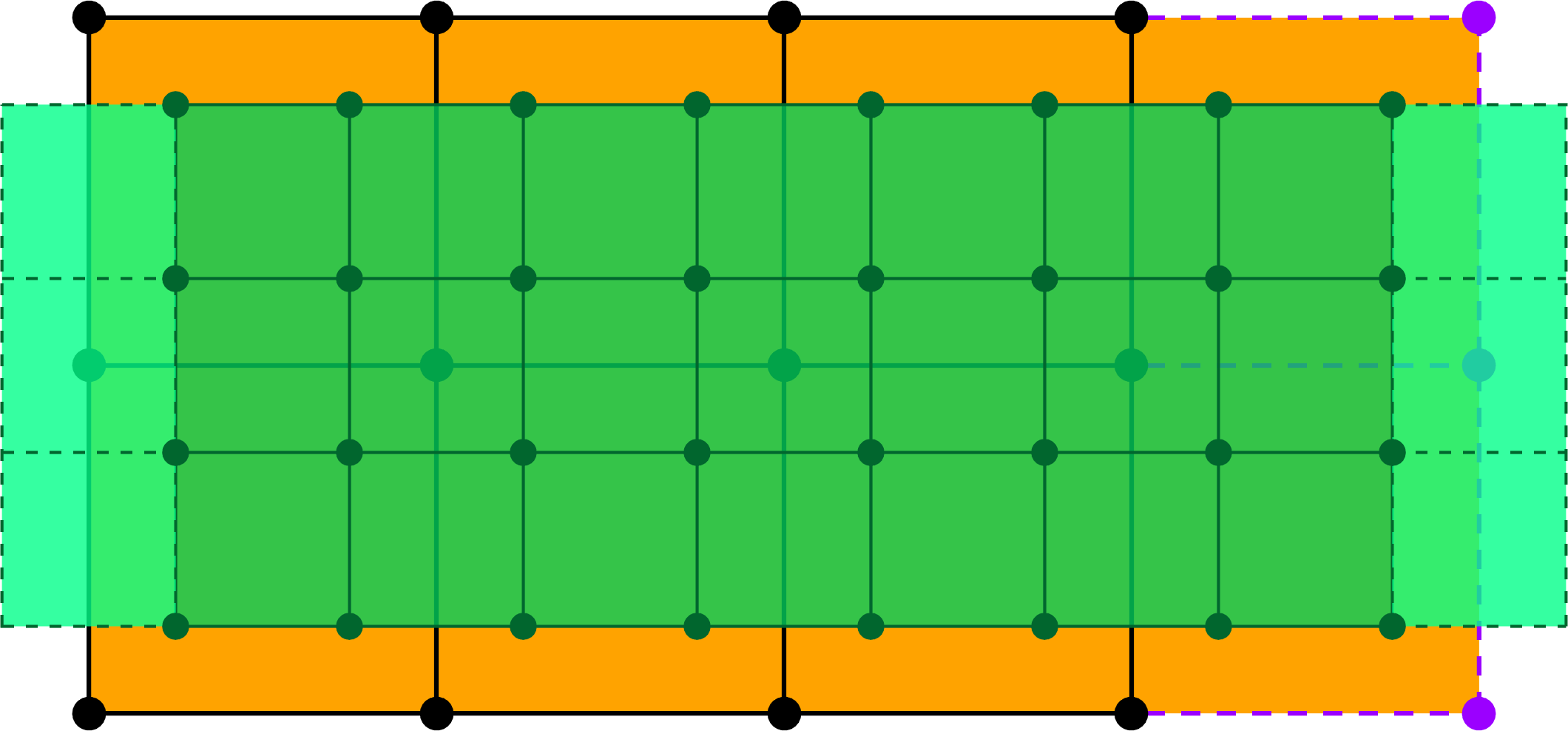
A subdivision step, surface closed in the $u$ direction.
Implementation
As before, the surfaces are represented via three coordinate matrices X, Y, Z. Apply the algorithm to each matrix individually.
The openness/closedness of a surface in a particular direction is controled via the parameters u_closed, v_closed (these are read from the input file).
Start by implementing the algorithm for a surface closed in both directions as this is easier to do; test on [torus]. Don’t forget to use the modulo arithmetic where needed. Then, think about what needs to be changed if the surface is open in one or both directions.
ToDo
- Implement one step of the above subdivision algorithm for closed uniform B-spline surfaces.
[torus] - Modify you implementation for surfaces which are open: either in one direction only
[cylinder]or in both directions[grid].