TP8 : Uniform B-splines as Subdivision Surfaces
Code
Algorithm
Much like in the curve case (recall Chaikin in TP4 or Lane-Riesenfeld in TP5), a uniform bi-quadratic B-spline surface ($k=2,l=2$) can be evaluated by iterative subdivision of the initial control net $V^0_{i,\;j}$. Here’s the algorithm to perform one step of the subdivision.
At the $k$-th iteration, for each cell of the grid composed of the vertices $V^k_{i,\;j}$ $V^k_{i+1,\;j}$ $V^k_{i,\;j+1}$ $V^k_{i+1,\;j+1}$ we define a new grid as follows
\[\begin{array}{ll} V^{k+1}_{2i,\;2j} &= \frac1{16} \left( 9V^k_{i,\;j} + 3V^k_{i+1,\;j} + 3V^k_{i,\;j+1} + 1V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i+1,\;2j} &= \frac1{16} \left( 3V^k_{i,\;j} + 9V^k_{i+1,\;j} + 1V^k_{i,\;j+1} + 3V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i,\;2j+1} &= \frac1{16} \left( 3V^k_{i,\;j} + 1V^k_{i+1,\;j} + 9V^k_{i,\;j+1} + 3V^k_{i+1,\;j+1} \right), \\ V^{k+1}_{2i+1,\;2j+1} &= \frac1{16} \left( 1V^k_{i,\;j} + 3V^k_{i+1,\;j} + 3V^k_{i,\;j+1} + 9V^k_{i+1,\;j+1} \right). \end{array}\]Important: If the surface is closed (cyclic) in the direction $u$, the subscripts $\scriptstyle i+1$ of $V^k$ are taken modulo the number of vertices in the direction $u$. The same applies for the direction $v$ and the subscripts $\scriptstyle j+1$.
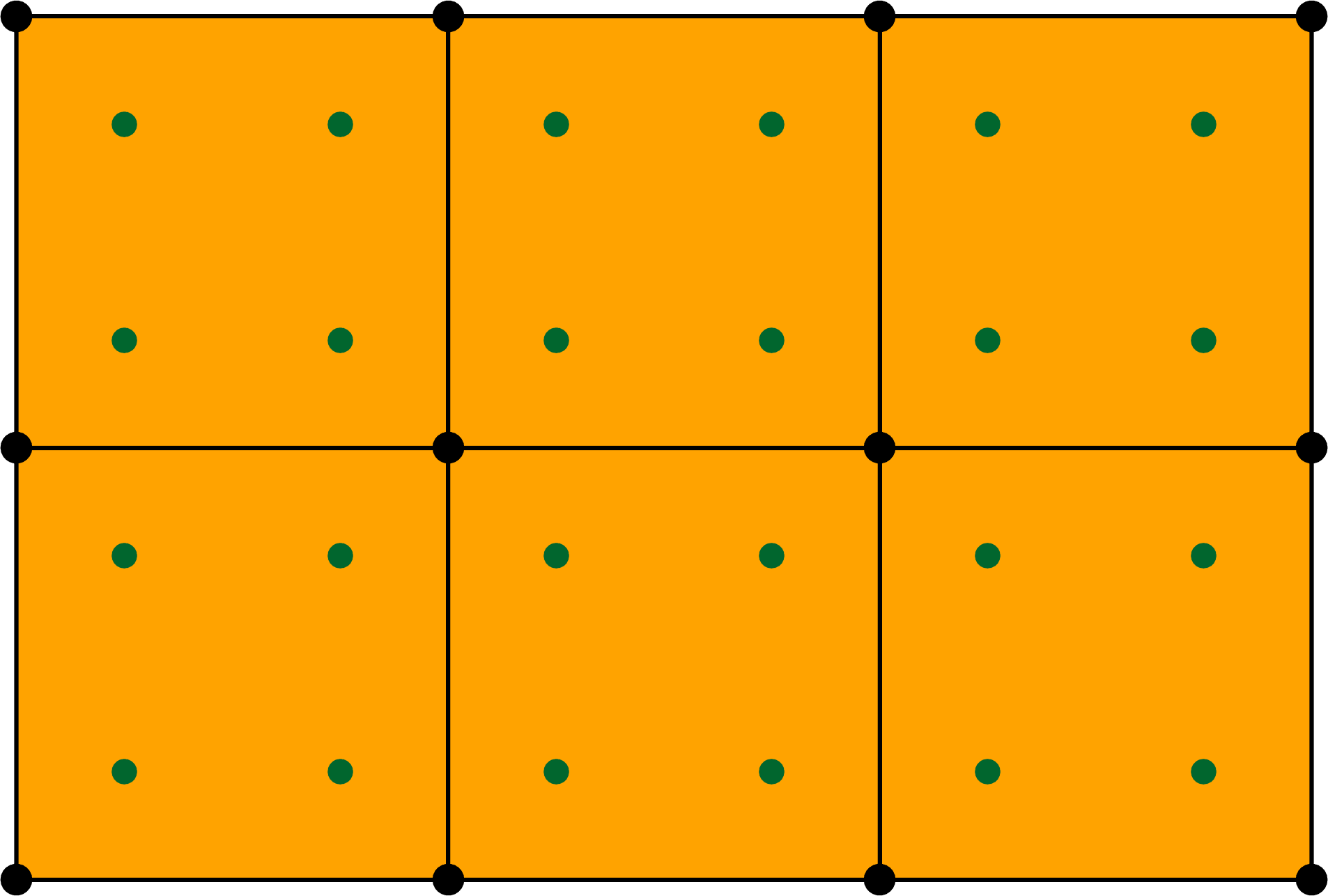
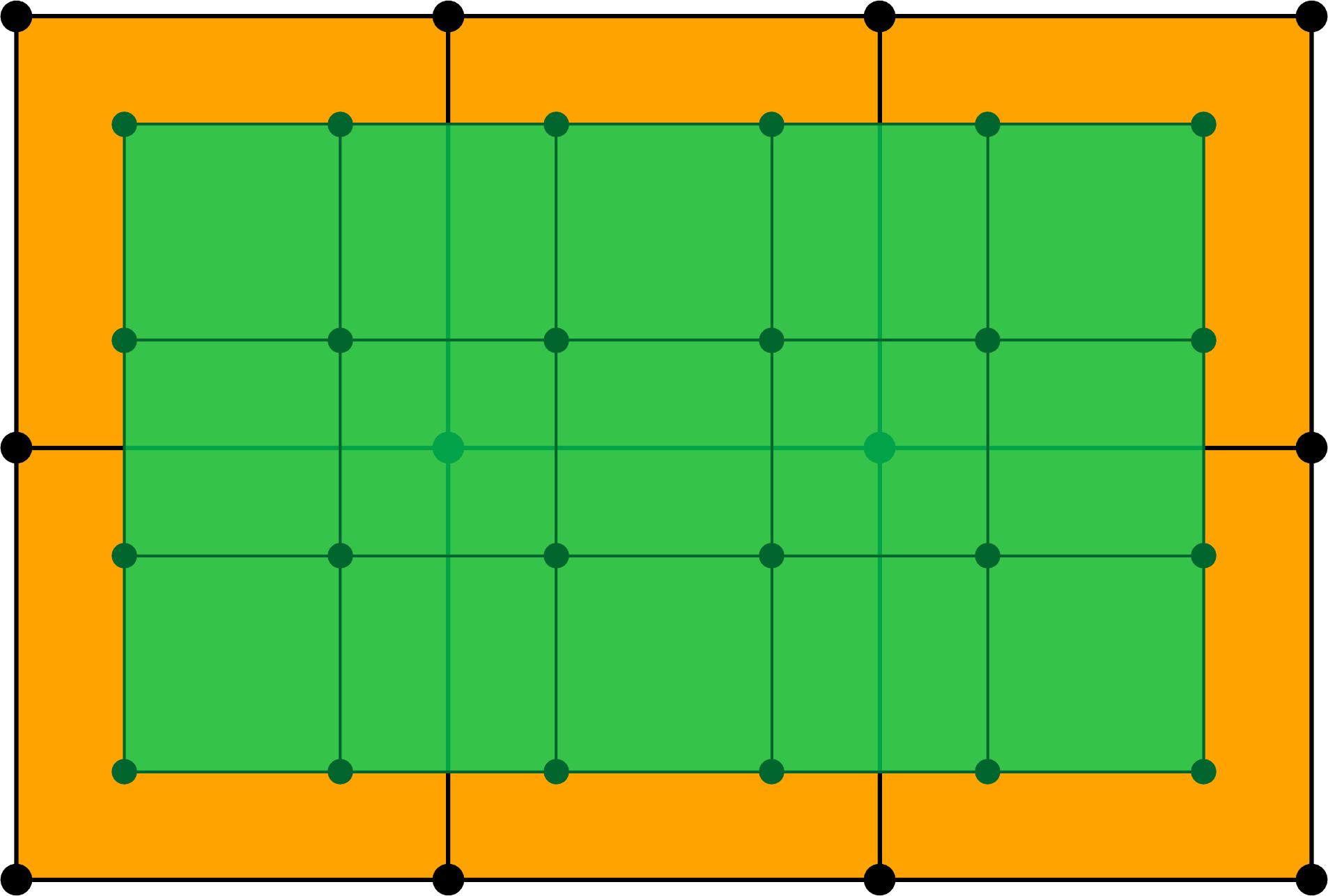
A subdivision step, open surface.
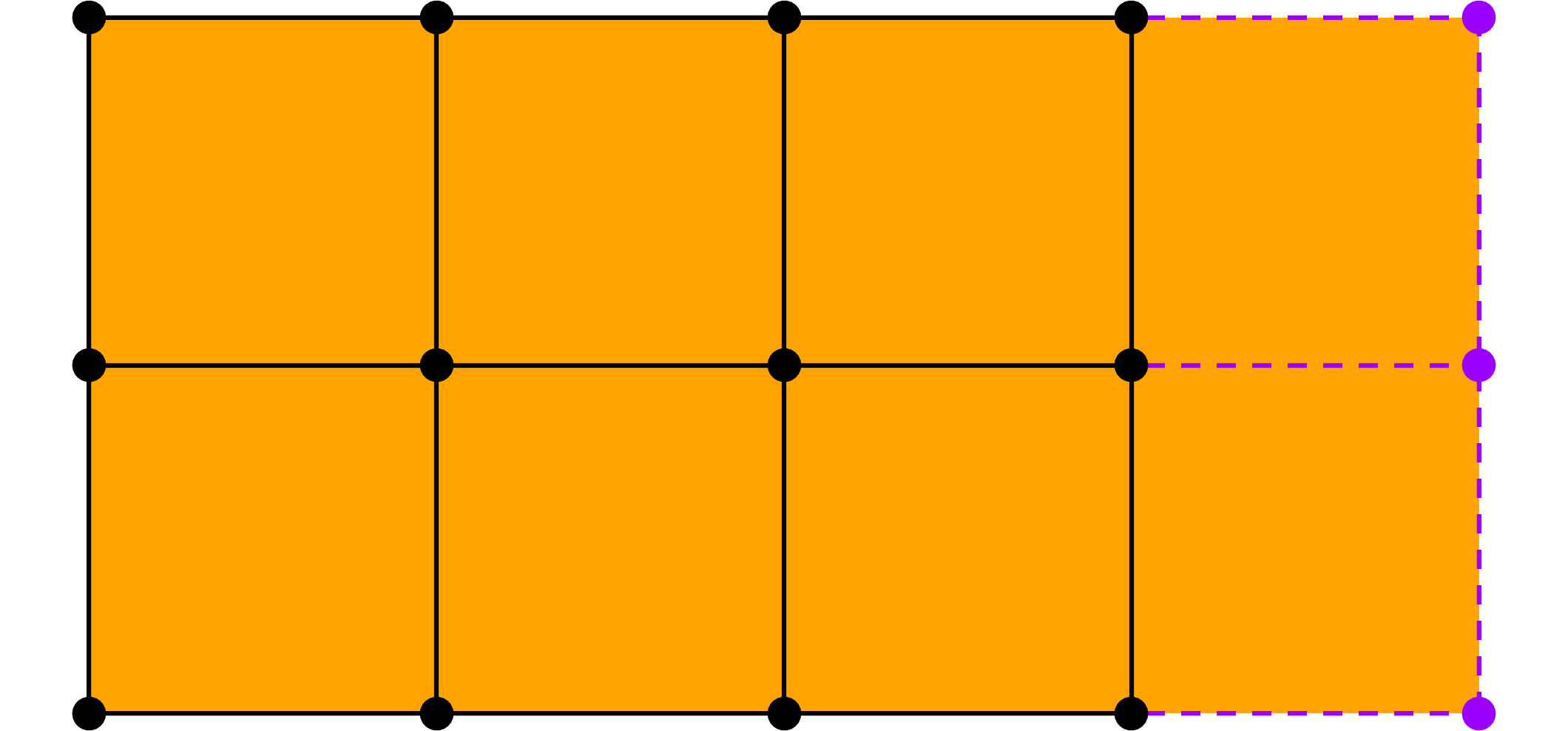

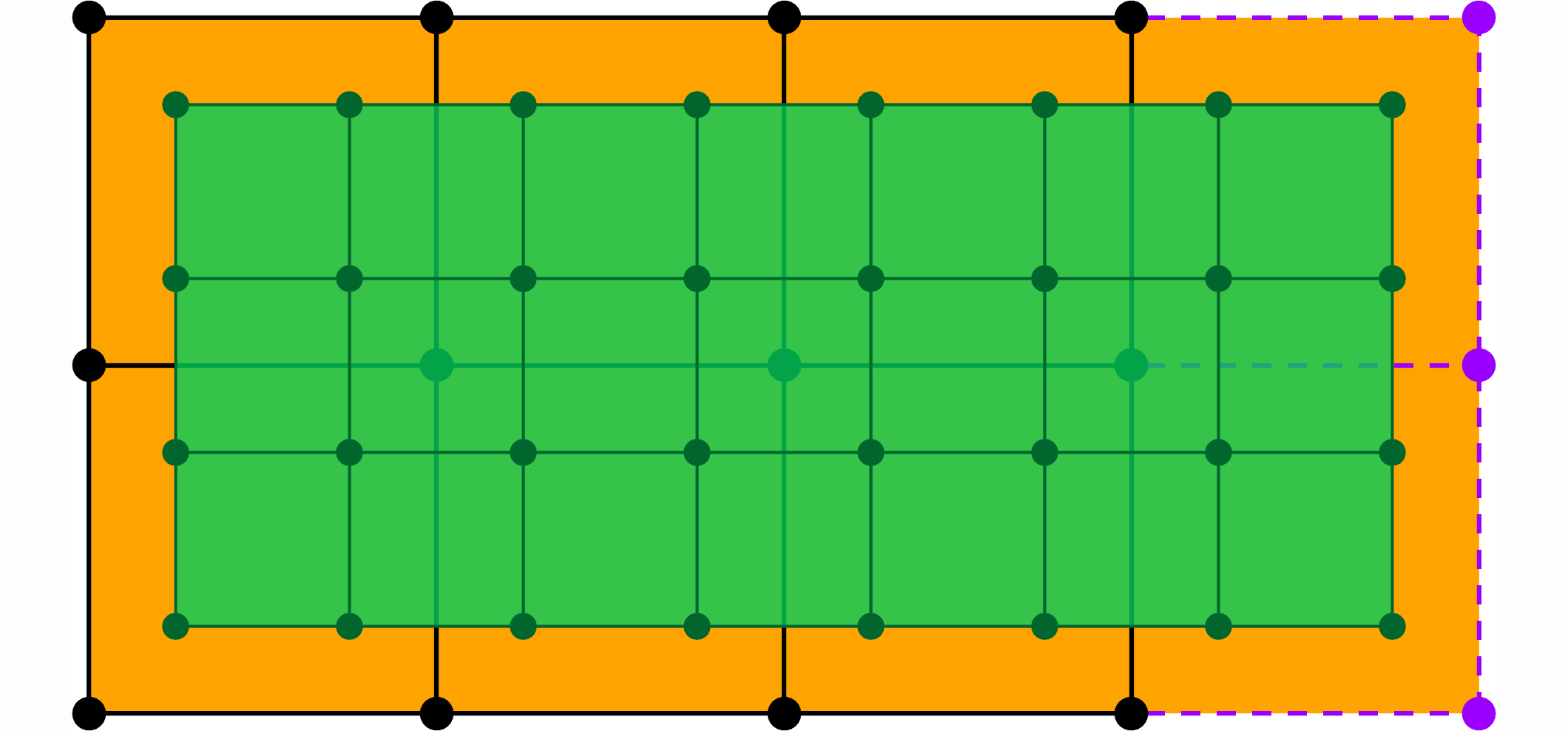
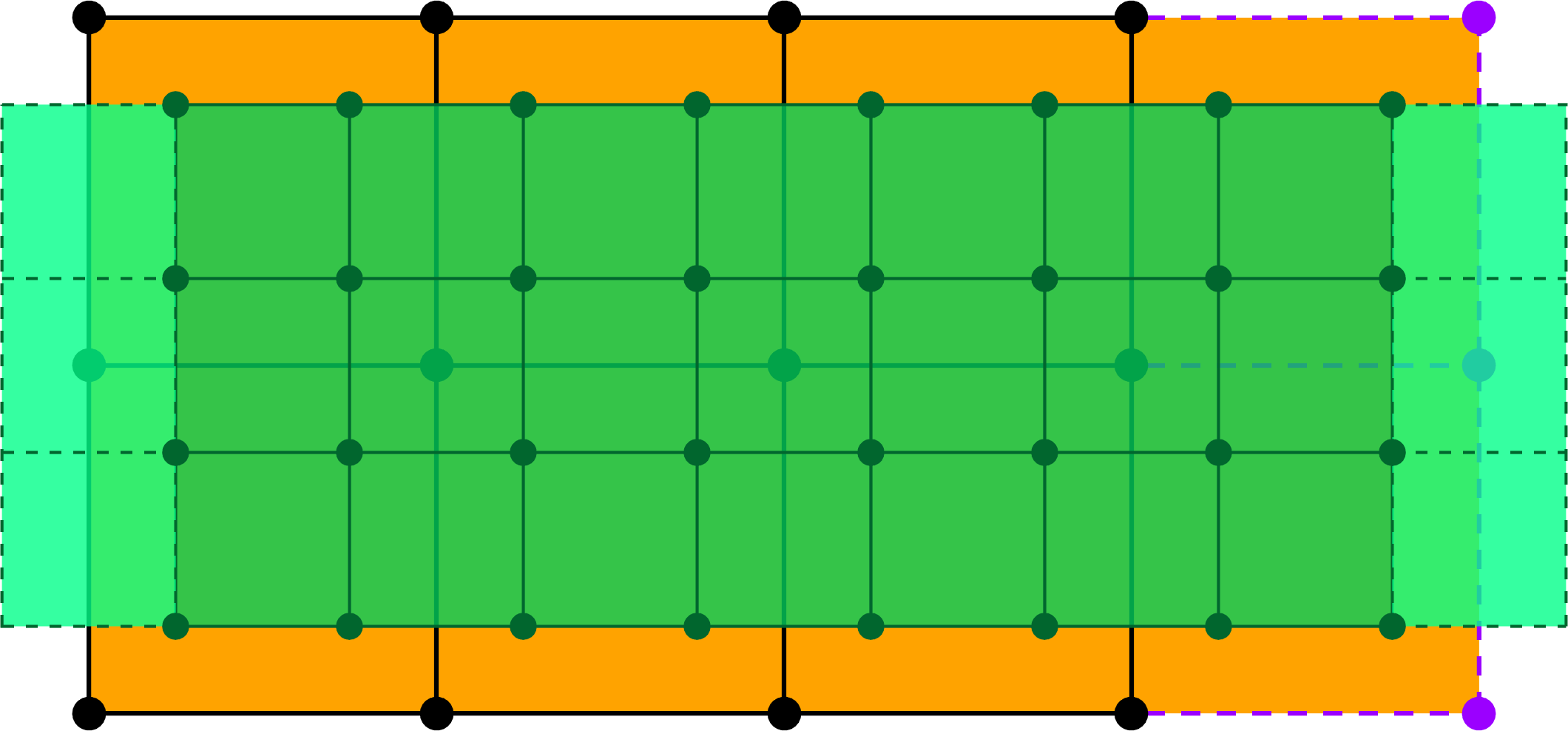
A subdivision step, surface closed in the $u$ direction.
ToDo
- Implement one step of the above subdivision algorithm for closed uniform B-spline surfaces (
torus). - Modify you implementation for surfaces which are open: either in one direction (
cylinder) or in both directions (grid,terrain). - Experiment with parameters in
GenerateRandomTerrain(). - [bonus] Catmull–Clark subdivision scheme produces bicubic B-spline surfaces. Although originally devised for quad-meshes with arbitrary topology, it work as well for uniform topologies (the ones we use in this TP). Implement this algorithm and compare the results with biquadratic surfaces. For more details of the algo, see the wikipedia page and also this article.