Tibor Stanko
TP9 submission deadline is Thursday, 13/04/2017 at 23:59. The TP on Friday 14/04 will start at 13:30 (instead of 15:15).

.geonum2017

  1. Bézier curves
  2. Bézier splines
  3. B-splines
  4. Subdivision curves
  5. Lane-Riesenfeld
  6. Bézier surfaces
  7. B-spline surfaces
  8. Subdivision B-surfaces
  9. Triangle mesh subdivision

TP1 : Bézier curves, De Casteljau’s algorithm

3 February 2017 in

Bézier curves

A degree $n$ Bézier curve takes the form

\[\mathbf x(t) = \sum_{i=0}^{n} \mathbf b_i B_i^n(t) \qquad t \in [0,1]\]

where

\[B_{i}^{n}(t) = \begin{pmatrix}n \\ i\end{pmatrix} (1-t)^{n-i} t^i\]

are the degree $n$ Bernstein polynomials, and the binomial coefficients are defined as

\[\begin{pmatrix}n \\ i\end{pmatrix} = \frac{n!}{(n-i)! i!}.\]

The Bézier points $\mathbf b_i \in \mathbb R^d$ form the control polygon.

De Casteljau’s algorithm

  • input Bézier points $\mathbf b_i$ for $i = 0, \dots, n$, and parameter $t \in [0,1]$.
  • output The point $\mathbf b_0^n$ on the curve.

  • compute Set $\mathbf b_i^0 = \mathbf b_i$ and compute the points

    \[\mathbf b_i^k (t) = (1-t) \mathbf b_i^{k-1} + t \mathbf b_{i+1}^{k-1} \qquad \text{for} \qquad k=1,\dots,n, \quad i=0,\dots,n-k.\]

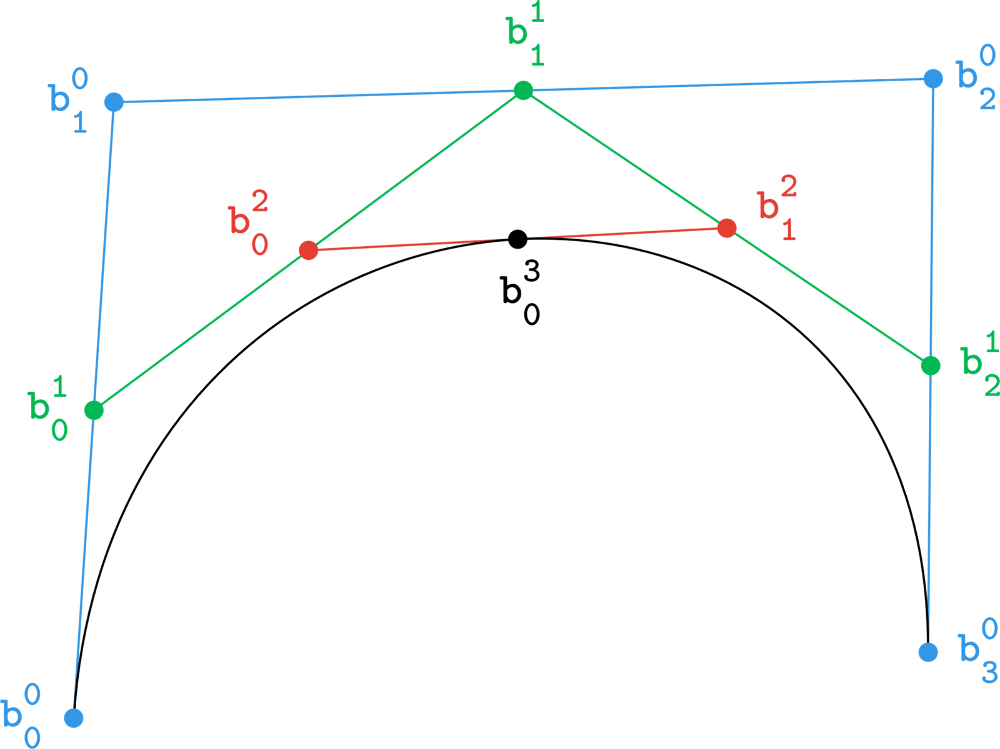
Visualisation of the steps of the De Casteljau's algorithm

Visualisation of the steps of the De Casteljau’s algorithm, $t=0.5$.

The De Casteljau’s algorithm provides an efficient means for evaluating a Bézier curve $\mathbf{x}(t)$. It is useful to look at this algorithm in its schematic form. For a cubic curve ($n=3$):

\[\begin{array}{ccccccc} \mathbf b_0 = \mathbf b_0^0 & & & & & & \\ & \ddots & & & & & \\ \mathbf b_1 = \mathbf b_1^0 & \dots & \mathbf b_0^1 & & & & \\ & \ddots & & \ddots & & & \\ \mathbf b_2 = \mathbf b_2^0 & \dots & \mathbf b_1^1 & \dots & \mathbf b_0^2 & & \\ & \ddots & & \ddots & & \ddots & \\ \mathbf b_3 = \mathbf b_3^0 & \dots & \mathbf b_2^1 & \dots & \mathbf b_1^2 & \dots & \mathbf b_0^3 = \mathbf x(t) \end{array}\]

Animation of the De Casteljau's algorithm for a quintic curve

Animation of the De Casteljau’s algorithm for a quintic curve ($n=5$).

Code

ToDo

  1. Implement the De Casteljau algorithm and use it to evaluate the Bézier curves in the data folder. Visualise the curves together with their control polygons.
  2. Try varying the sampling density. How many samples are needed to give the impression of a smooth curve?
  3. Pick one dataset and visualise all intermediate polygons $\mathbf b_i^k$ from the De Casteljau algorithm for a fixed parameter, for instance $t=0.5$.
    Hint: each column in the above schema represents one such polygon.

Resources